Utiliser un arbre pondéré

Pour calculer les probabilités des événements dans cet exercice, nous utilisons un arbre pondéré. Nous avons des informations sur les probabilités et nous souhaitons en déduire d'autres. Nous savons que Naomi se rendra au lycée en vélo ou en bus. Lorsqu'il fait beau, elle prend le vélo 8 fois sur 10, et lorsqu'il fait moche, elle prend le vélo 5 fois sur 10. De plus, dans sa ville, il y a 75% de journées ensoleillées. Nous prenons une journée au hasard où nous ne savons pas s'il fait beau ou non. Nous voulons déterminer la probabilité que l'événement E et l'événement V se produisent, ainsi que la probabilité que V se produise sachant que E se produit. 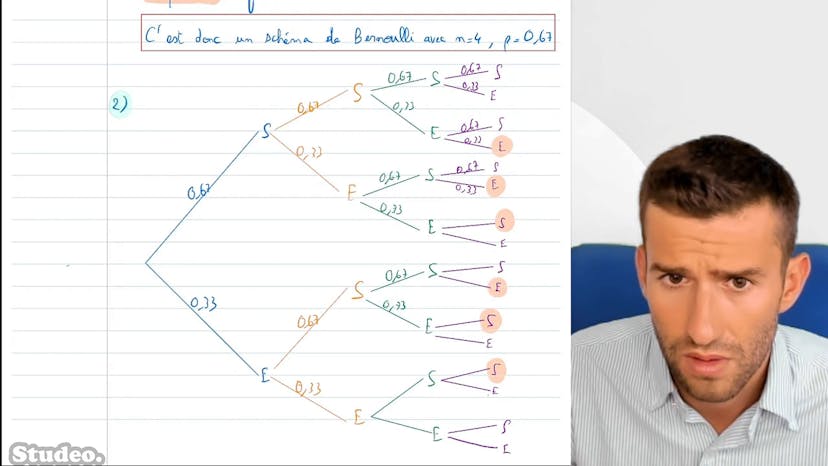Nous utilisons un arbre pondéré pour représenter les probabilités. Nous écrivons les probabilités associées à chaque nœud de l'arbre. Par exemple, la probabilité qu'il fasse beau est de 0.75 et la probabilité qu'il ne fasse pas beau est de 0.25. Ensuite, nous utilisons les informations pour remplir l'arbre pondéré. Par exemple, sachant qu'il fait beau, la probabilité que Naomi prenne le vélo est de 0.8, donc la probabilité qu'elle ne prenne pas le vélo est de 0.2. De la même manière, si le temps est mauvais, la probabilité qu'elle prenne le vélo est de 0.5 et la probabilité qu'elle prenne le bus est également de 0.5. Nous vérifions que la somme des probabilités pour chaque branche de l'arbre est toujours égale à 1. Maintenant, nous pouvons calculer les probabilités des événements. La probabilité que les événements E et V se produisent simultanément est calculée en utilisant la formule P(E ∩ V) = P(E) * P(V|E). Dans notre cas, cela donne 0.75 * 0.8 = 0.6, donc il y a 60% de chances que Naomi prenne le vélo s'il fait beau. Ensuite, nous voulons calculer la probabilité de l'événement V, c'est-à-dire la probabilité que Naomi prenne le vélo. Pour cela, nous utilisons la formule des probabilités totales, qui est P(V) = P(E) * P(V|E) + P(E') * P(V|E'). Dans notre cas, cela donne 0.75 * 0.8 + 0.25 * 0.5 = 0.725, donc il y a 72,5% de chances que Naomi prenne le vélo. Ceci résume les calculs de probabilités effectués à l'aide d'un arbre pondéré.