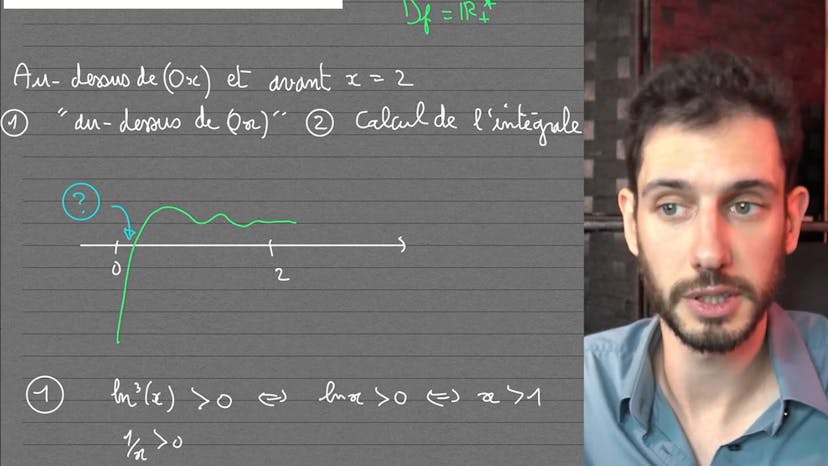Une intégrale facile en Terminale ?

Antonin, un professeur de maths spécialisé dans la préparation des étudiants aux universités américaines, explique un exercice du MIT. L'exercice consiste à calculer l'intégrale d'une expression comprenant des puissances et des variables. Antonin recommande de ne pas être intimidé par les termes compliqués et propose une stratégie pour aborder l'exercice. Il identifie certaines parties de l'expression comme des blocs distincts, ce qui facilite leur analyse. En donnant un nom à l'un de ces blocs, Antonin remarque une connexion entre une fonction U et sa dérivée, ce qui est utile pour résoudre l'exercice. Il applique ensuite une formule qui relie la dérivée d'une puissance U2X à la valeur alpha de cette puissance. En utilisant cette formule, Antonin détermine la valeur alpha originelle et obtient une forme simplifiée de l'expression. En intégrant cette forme simplifiée, il trouve la réponse finale de l'exercice. La solution est exprimée comme une intégrale de la primitive de l'expression entre 0 et 1, ce qui donne un résultat final de 8 racines de 2 moins 3 racines de 3. Antonin conclut en espérant que cette explication a été utile et propose de retrouver ses prochaines vidéos.