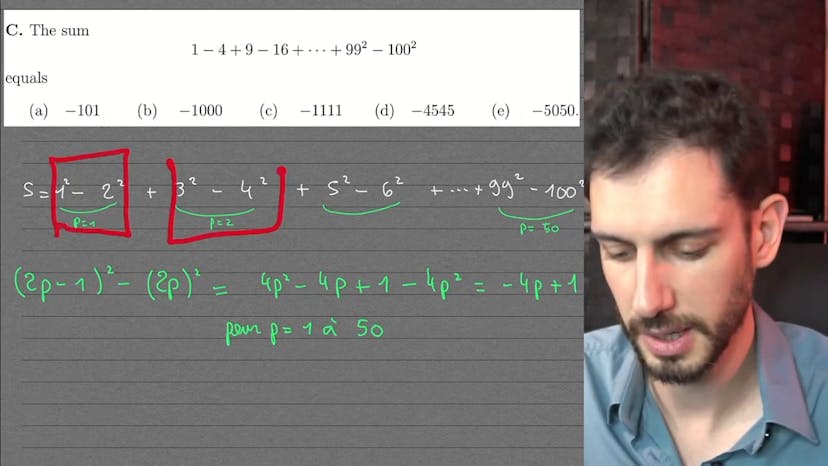
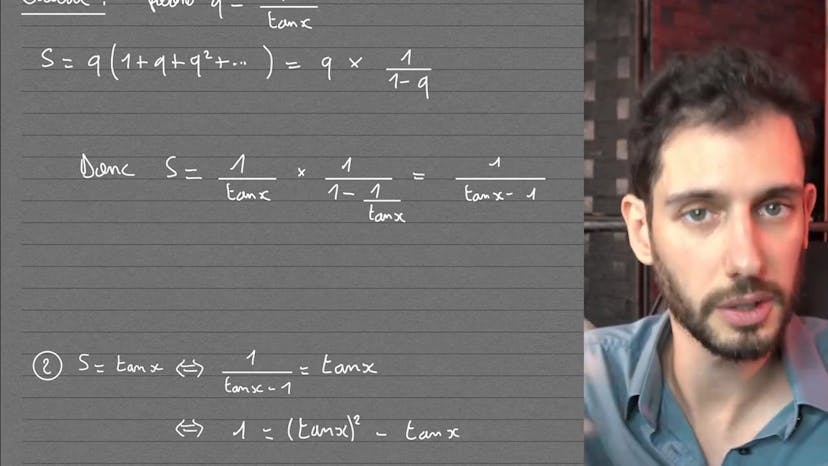Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens- Concours et examens UK
- Oxford Imperial MAT
- Cambridge
- Concours et examens US
- Concours et examens Français
- Bac et examens étrangers
Terminale
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens- Concours et examens UK
- Oxford Imperial MAT
- Cambridge
- Concours et examens US
- Concours et examens Français
- Bac et examens étrangers
Terminale
Une fonction trigo bien moche !
Bonjour à tous ! Dans cette vidéo, nous allons analyser une question du Math Admission Test d'Oxford en 2020. La question est la suivante : "Quelle est la plus grande valeur atteinte par l'expression 3 cos²x plus sin²x plus 1 ?".
La première étape consiste à simplifier l'expression. Pour cela, nous allons utiliser une relation fondamentale de la trigonométrie qui nous dit que cos²x équivaut à 1-sin²x. En remplaçant cos²x par cette équation, nous obtenons l'expression 3-3sin²x plus 2sin²x plus 1, que nous simplifions pour obtenir 3-sin²x plus 2sin²x plus 4.
Nous remarquons qu'il y a un polynôme du second degré caché dans cette expression. Pour faciliter les calculs, nous posons une variable intermédiaire grand x égale à sin²x. Nous notons également que grand x doit être compris entre -1 et 1.
Ainsi, nous avons une nouvelle expression Q2x égale à -3 fois grand x² plus 2x plus 4. Nous devons déterminer la valeur maximale atteinte par cette fonction. Comme il s'agit d'un polynôme du second degré, nous savons qu'elle atteint son maximum. En utilisant la formule du maximum d'un polynôme du second degré, nous trouvons que le maximum est atteint en 1/3.
Nous pouvons calculer la valeur maximale en substituant 1/3 à x dans l'expression Q. Après les calculs, nous obtenons que Q de 1/3 est égal à 13/3.
Ainsi, la réponse à la question est 13/3. J'espère que ce résumé était clair et n'hésitez pas à poser des questions dans les commentaires. À bientôt pour une prochaine vidéo !