Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Observation de la planète Mars (3)
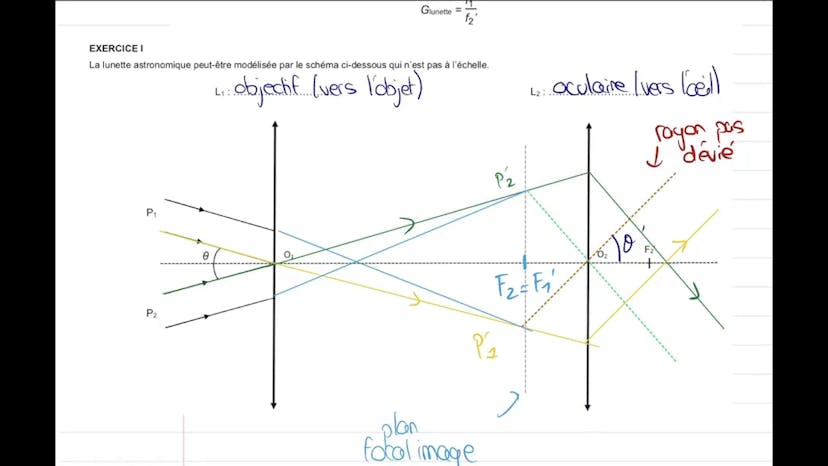
Dans cette vidéo, nous terminons l'exercice 1 du sujet de bac qui porte sur l'observation de la planète Mars. Les deux premières parties de cet exercice ont porté sur l'étude de Mars du point de vue optique. Nous avons utilisé la lunette astronomique pour déduire le diamètre de Mars. Dans cette dernière partie, nous nous intéressons à la masse de Mars en utilisant les lois de Newton.
Nous assimilons Mars à une sphère de diamètre dm et de masse M, environ dix fois plus petite que celle de la Terre. Pour déterminer cette masse, nous observons le satellite naturel de Mars, Phobos, et utilisons les lois de Newton. Nous connaissons la période de révolution de Phobos, sa trajectoire et le fait qu'il est soumis uniquement à la force de gravitation de Mars.
Pour déterminer la vitesse de Phobos sur son orbite circulaire, nous utilisons la deuxième loi de Newton avec un bilan des forces. Nous utilisons le système Phobos dans le référentiel centré sur la masse de Mars et faisons un bilan des forces. Nous déduisons que la force gravitationnelle est égale à la masse multipliée par l'accélération.
Nous utilisons ensuite la formule de l'accélération dans le repère de Freinet pour les mouvements de planètes circulaires, qui nous permet d'exprimer l'accélération en fonction de la vitesse et du rayon de l'orbite. En isolant la vitesse, nous obtenons l'égalité v²/rmp = gm/rmp², où g est la constante de gravitation et mm est la masse de Mars.
Pour déterminer la masse de Mars, nous devons prendre des initiatives et présenter notre méthode. Nous connaissons la période de révolution de Phobos et le rayon de son orbite. Nous avons également établi une relation entre la vitesse et la masse de Mars. Nous utilisons la propriété d'une orbite circulaire pour établir le lien entre la vitesse, la période et le rayon. En égalant les deux expressions de la vitesse obtenues précédemment, nous pouvons isoler la masse de Mars. En résolvant numériquement, nous obtenons une valeur de 464 x 10^23 kg, environ dix fois plus grande que la masse de la Terre, ce qui est cohérent.
En conclusion, cet exercice nous a permis d'utiliser les lois de Newton pour déterminer la masse de la planète Mars en observant son satellite Phobos.