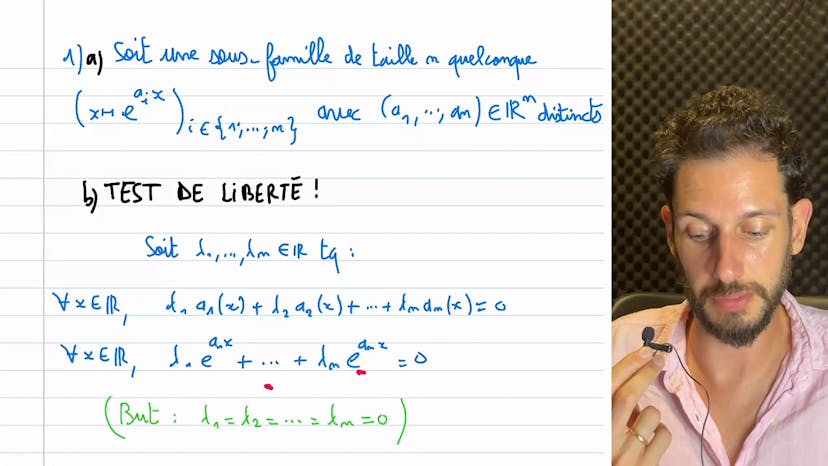Famille libre

Ce cours traite de la notion de liberté ou de liaison d'une famille de vecteurs. L'objectif est de déterminer si une famille donnée est libre ou liée en utilisant une méthode classique. On suppose l'existence d'une combinaison linéaire qui lie tous les éléments de la famille ensemble, et on cherche à trouver une contradiction à cette hypothèse. Si une telle combinaison linéaire existe, alors tous les coefficients doivent nécessairement être égaux à zéro, ce qui prouve que la famille est libre. On écrit donc cette combinaison linéaire et on la traduit en un système d'équations, qu'on résout pour trouver les coefficients lambda et mu. Si on trouve que tous les coefficients sont nuls, cela signifie que la famille est libre. On répète cette démarche pour différentes paires de vecteurs de la famille pour déterminer si elles sont libres ou liées. Enfin, pour déterminer si la famille de vecteurs dans son ensemble est libre ou liée, on rédige une nouvelle combinaison linéaire en introduisant des coefficients lambda1, lambda2, et lambda3, et on cherche à trouver si cette combinaison linéaire a une solution unique. Si elle en a, alors la famille est liée, sinon elle est libre. Dans l'exemple donné, on observe que la famille v1, v2, v3 est liée, car il est possible de trouver une combinaison linéaire telle que -2v1 + v2 - v3 = 0, ce qui montre que les trois vecteurs sont liés dans un plan et qu'aucun d'entre eux ne sort de ce plan. Cela signifie que la famille ne couvre pas l'ensemble de l'espace, ce qui fait qu'elle est liée.