 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Fonctions
Seconde

Comparer x et sa racine
Dans cet exercice, on apprend à déterminer la position relative de deux courbes en étudiant le signe de la différence f(x) - g(x). En factorisant cette expression, on peut facilement déterminer son signe à partir d'un tableau de signes. Pour cela, on détermine d'abord le signe de racine de x - 1, qui est positif pour x>1 et négatif pour x<1. Ensuite, on peut construire le tableau de signes de f(x) - g(x) et déterminer quelle courbe est au-dessus de l'autre selon le signe obtenu.
Maths
Fonctions
Seconde

Tableau de signes avec du x²
Apprenez à résoudre les inéquations contenant des puissances supérieures à 1 en suivant ces étapes : mettre tous les termes d'un côté pour avoir 0 de l'autre côté, factoriser l'équation, entrer les valeurs de x pour lesquelles les facteurs s'annulent dans un tableau de signes, déterminer les signes de chaque facteur, puis identifier les valeurs de x pour lesquelles l'expression est positive. En appliquant cette méthode à l'inéquation x² + 4x ≥ -3x, nous obtenons que x appartient à l'intervalle moins l'infini moins 7, union 0 plus l'infini.
Maths
Fonctions
Seconde
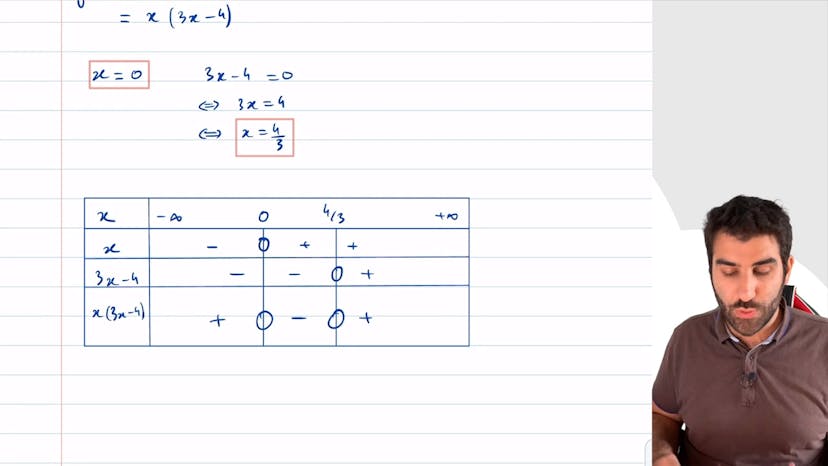
Factorisation et tableau de signes
Cet exercice consiste à dresser le tableau de signe d'une fonction à partir de son expression factorisée. Il est important de factoriser avant de faire le tableau de signe. On cherche ensuite les valeurs pour lesquelles chaque facteur s'annule (x=0 et x=4/3 dans cet exemple), puis on remplit les signes en se rappelant la règle de signes pour les expressions affines et en utilisant la règle de signes pour le produit final.
Maths
Fonctions
Seconde
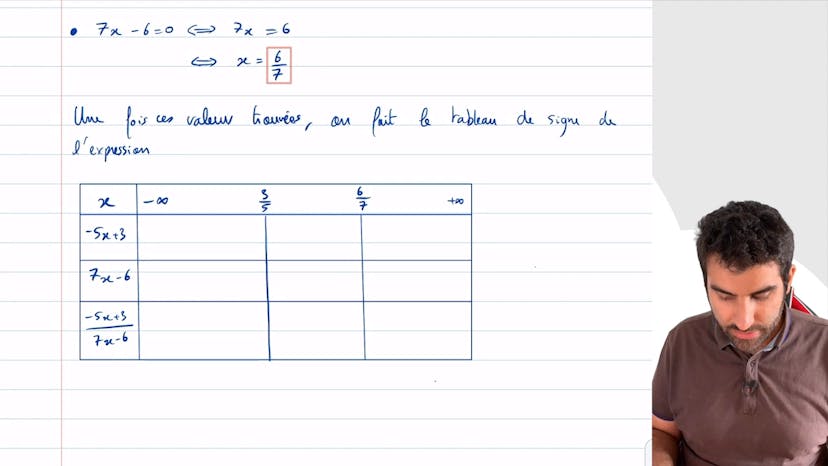
Tableau de signes pour un quotient
Dans cet exercice, il est expliqué comment déterminer le signe d'une fonction. Pour ce faire, il faut d'abord résoudre les équations pour trouver les valeurs de x pour lesquelles le numérateur et le dénominateur s'annulent. Puis, on crée un tableau de signes en mettant sur chaque ligne les valeurs de x pertinentes, les facteurs de l'expression et le bilan du produit ou quotient. Les bornes de l'ensemble de définition sont également indiquées. Les zéros sont placés à l'endroit où chaque ligne s'annule. Les lignes affiliées à une expression affine, c'est-à-dire celle ax+b, prennent le signe positif avant zéro et le signe négatif après. Une double barre est utilisée pour les valeurs interdites. Ensuite, on utilise la règle des signes pour remplir la dernière ligne du tableau. À partir de ce tableau, on peut déduire le signe de la fonction.


