 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Stats et Probas
Seconde

Renverser un pourcentage : TVA
Dans cet exercice, nous allons apprendre à calculer le prix hors taxe d'un produit en utilisant un taux de TVA de 20%. Pour trouver le prix TTC, nous multiplions le prix hors taxe par 1,20 sur 100. Pour trouver le prix hors taxe à partir du prix TTC, nous divisons le prix TTC par 1,20. Par exemple, si le prix affiché au magasin est de 642€ TTC, le prix hors taxe est de 535€ en divisant par 1,2.
Maths
Stats et Probas
Seconde

Augmentation en pourcentage
Dans cet exercice de calcul de prix, nous devons déterminer le nouveau prix d'une baguette dans une boulangerie suite à une augmentation de 10%. Pour cela, nous utilisons une méthode qui implique de multiplier le prix initial par 1 plus x sur 100, où x est le pourcentage d'augmentation. Dans notre cas, le nouveau prix est de 99 centimes après avoir multiplié le prix initial de 90 centimes par 1,10.
Maths
Stats et Probas
Seconde

Fonction de prix et pourcentage
Dans cet exercice de mathématiques, nous apprenons à généraliser une augmentation de prix de tous les produits d'un magasin. Le gérant du supermarché a décidé d'augmenter tous les prix de 2%. Nous notons x comme le prix d'un produit, f(x) sera le nouveau prix. Pour calculer une augmentation de x%, on multiplie par 1+x/100. Dans ce cas, l'augmentation de 2% est égale à multiplier par 1,02. Donc, f(x) est égale à 1,02x. La méthode générale pour cette augmentation inconnue est représentée par la variable x. L'expression finale est f(x) = 1,02x.
Maths
Stats et Probas
Seconde
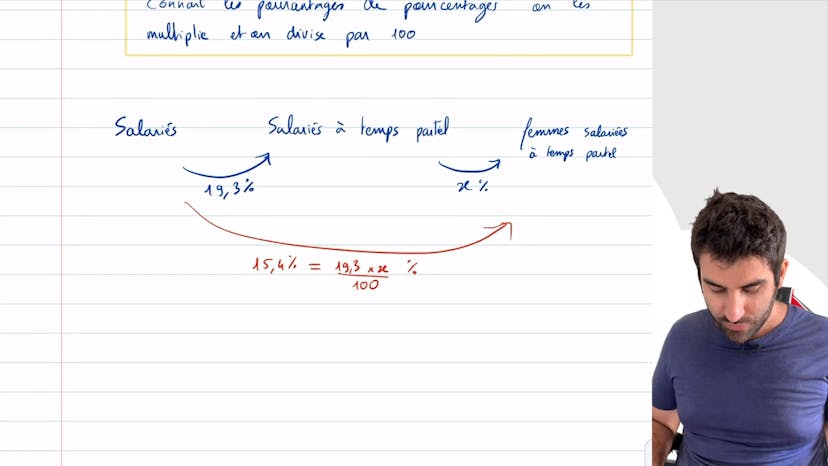
Pourcentage de pourcentage ?
Dans cet exercice, on apprend comment déterminer une proportion de proportions. On applique la méthode qui consiste à multiplier et diviser par 100 pour trouver un pourcentage global en connaissant les pourcentages de pourcentages. On nous donne des informations sur les salariés à temps partiel et les femmes salariées à temps partiel. On apprend que 19,3% des salariés sont à temps partiel et que la proportion de femmes salariées à temps partiel parmi l'ensemble des salariés est de 15,4%. En utilisant la méthode du pourcentage global, on trouve que 15,4% est égal à 19,3 fois x sur 100 pour 100, ce qui permet de résoudre l'équation et d'isoler x. Ainsi, on apprend que parmi les salariés à temps partiel, il y a 70,79% de femmes.
Maths
Stats et Probas
Seconde

Pourcentage sur 3 ans
Dans cet exercice, nous apprenons comment faire une hausse pour rattraper une hausse avec un retard de 3 ans. Nous sommes confrontés à une situation dans laquelle les prix augmentent de 2% chaque année, mais le salaire de Nora n'a pas augmenté. Ainsi, pour déterminer l'augmentation de X%, nous devons multiplier par 1 plus X sur 100. Une augmentation de 2% correspond donc à une multiplication par 1,02 chaque année. Comme le salaire de Nora n'a pas augmenté depuis 3 ans, nous avons multiplié par 1,02 x 1,02 x 1,02, ce qui correspond à 1,0612. Donc, pour rattraper cette hausse de salaire, il faut multiplier le salaire de Nora par 1,0612, soit une augmentation de 6,12%.


