Tous les sujets
Maths
Physique-Chimie
Corrigés de BAC- Révisions Maths lycée
Prépa Examens
Concours et examens US
Terminale
Une intégrale facile en Terminale ?
Antonin, un professeur de maths spécialisé dans la préparation des étudiants aux universités américaines, explique un exercice du MIT. L'exercice consiste à calculer l'intégrale d'une expression comprenant des puissances et des variables. Antonin recommande de ne pas être intimidé par les termes compliqués et propose une stratégie pour aborder l'exercice. Il identifie certaines parties de l'expression comme des blocs distincts, ce qui facilite leur analyse. En donnant un nom à l'un de ces blocs, Antonin remarque une connexion entre une fonction U et sa dérivée, ce qui est utile pour résoudre l'exercice. Il applique ensuite une formule qui relie la dérivée d'une puissance U2X à la valeur alpha de cette puissance. En utilisant cette formule, Antonin détermine la valeur alpha originelle et obtient une forme simplifiée de l'expression. En intégrant cette forme simplifiée, il trouve la réponse finale de l'exercice. La solution est exprimée comme une intégrale de la primitive de l'expression entre 0 et 1, ce qui donne un résultat final de 8 racines de 2 moins 3 racines de 3. Antonin conclut en espérant que cette explication a été utile et propose de retrouver ses prochaines vidéos.
Prépa Examens
Concours et examens US
Terminale
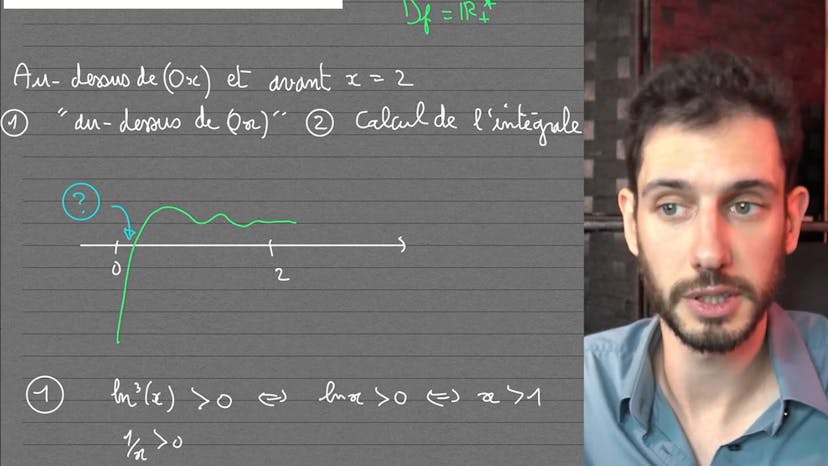
Aire sous une courbe !
Bonjour à tous ! Aujourd'hui, je vais vous résumer un cours sur un exercice du MIT concernant le calcul d'une intégrale. Tout d'abord, l'énoncé demande de trouver l'aire sous la courbe définie par la fonction log de X au cube sur X, située au-dessus de l'axe OX et à gauche de la ligne verticale X=2.
Pour résoudre cet exercice, nous devons effectuer deux étapes. La première consiste à comprendre à partir de quel point nous devons commencer à calculer notre intégrale, et la deuxième étape consiste simplement à effectuer le calcul lui-même.
La fonction log de X est définie pour les réels strictement positifs, donc l'ensemble de définition de cette fonction est R+*. Nous devons donc trouver le point à partir duquel la courbe est positive. Nous pouvons déterminer cela en étudiant la positivité de log de X au cube. Nous constatons que log de X au cube est positif si et seulement si log de X est positif. Puisque nous connaissons les variations de log de X, nous savons que cette fonction est positive pour les valeurs de X strictement supérieures à 1.
Maintenant que nous avons déterminé le point de départ de notre intégrale, nous pouvons l'écrire sous la forme suivante : l'intégrale de log de X au cube fois 1 sur X, entre 1 et 2. Nous remarquons que 1 sur X est la dérivée de log de X. Ainsi, nous pouvons appliquer la formule classique de l'intégrale. En posant u=log de X, nous obtenons une structure de la forme u au cube fois u prime. Nous savons que l'intégrale de cette primitive est u puissance 4 divisé par 4. En appliquant cette formule, nous obtenons comme résultat log de 2 puissance 4 divisé par 4 au point 2, et log de 1 qui est égal à 0 au point 1.
Finalement, nous trouvons que l'aire sous la courbe, au-dessus de l'axe OX et à gauche de la ligne X=2, est égale à log de 2 puissance 4 divisé par 4. J'espère que ce résumé SEO-friendly était clair et je vous dis à bientôt pour une prochaine vidéo !
Prépa Examens
Concours et examens US
Terminale
Une tache d'huile sur un lac
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens US
Terminale
Une tache d'huile sur un lac
Aucun résumé n'est disponible pour cette vidéo
