Cours d'apprentissage en ligne

Onde stationnaire et modes propres

Cette vidéo traite des modes propres associés à une onde stationnaire. Un mode propre correspond à une manière naturelle d'osciller pour un système physique, qui dépend des conditions dans lesquelles il se trouve. L'onde stationnaire étudiée est sur une corde et est décrite par la relation y(x,t) = y0 sin(ωt + φ) sin(kx + ψ), où y est la déformation verticale de la corde. Les conditions aux limites en x=0 et x=L permettent de quantifier la fréquence et le vecteur d'onde, qui correspondent au mode propre du système. L'expression du nème mode propre Yn de Xt en fonction de nLc Xt et de l'amplitude de ce mode propre Y0n est donnée. La quantification du vecteur d'onde est un concept important en physique qui se retrouve en mécanique quantique.

Onde stationnaire

La vidéo explique le modèle des ondes stationnaires en montrant que la superposition de deux ondes progressives sinusoïdales de même amplitude et de même pulsation qui se propagent dans des directions opposées donne une onde sinusoïdale. Pour y arriver, il utilise des formules de trigonométrie et montre que la superposition des deux ondes progressives donne une onde stationnaire, qui est une fonction de l'espace et du temps présentée comme le produit d'une fonction uniquement du temps et d'une fonction uniquement de l'espace. Cette première approche du modèle des ondes stationnaires sera développée dans les prochaines vidéos.

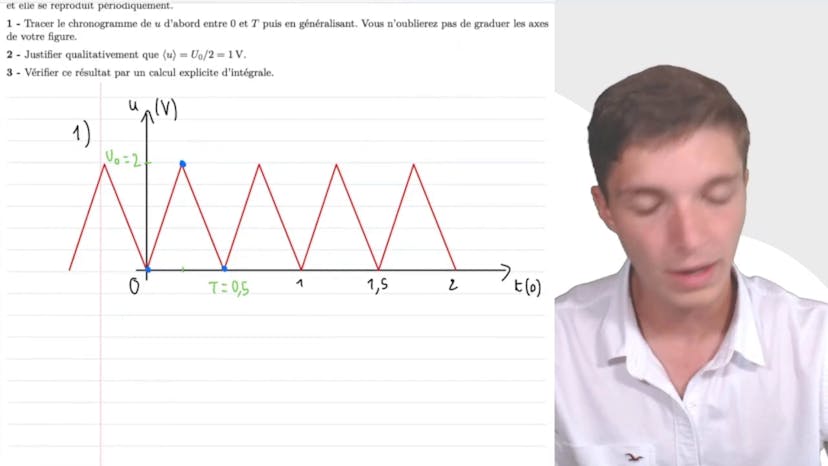
Signal triangle

Dans cette vidéo, nous étudions un signal triangle avec une tension U de t triangulaire comprise entre 0 et U0. Le signal a une période T qui est égal à 0,50s et est défini par une équation. Pour tracer le chronogramme, on voit que le signal augmente de manière linéaire avec une pente de 2U0 sur T avant de diminuer de la même façon pour revenir à 0 lorsque T vaut T. La valeur moyenne de U est équivalente à U0 divisé par 2 et est donc égale à 1V. Cela peut être justifié qualitativement en considérant que chaque temps passé au-dessus de 1V est compensé par la même quantité de temps passé en-dessous de 1V. Cette valeur moyenne peut être calculée en utilisant l'intégrale de la définition de la valeur moyenne d'un signal périodique. Ce signal triangle est très utilisé expérimentalement dans les circuits électriques.

Premiers circuits

Cette vidéo aborde deux circuits électriques et comment déterminer la tension et l'intensité en fonction des grandeurs Eta, E et R. Dans le premier circuit, il y a deux résistances en série avec un générateur éteint. En utilisant les lois de diviseurs de courant et de tension et en travaillant sur les résistances équivalentes, on peut exprimer la tension au bord de la résistance en utilisant la loi d'Ohm. Dans le deuxième circuit, il y a deux générateurs (un de tension et un de courant) et on souhaite déterminer la tension et le courant. On peut utiliser les lois d'émail et des nœuds pour exprimer les grandeurs en fonction des autres grandeurs données et isoler les inconnues pour trouver la tension et l'intensité. Être à l'aise avec ces lois permet de déterminer précisément les tensions des dipôles.

Equivalence de circuits

Dans cette vidéo, nous cherchons à établir une équivalence de circuit entre un montage étoile et un montage en triangle en cherchant les résistances correspondantes. Nous exprimons la tension UAB en fonction des résistances et courants pour les deux montages en utilisant les lois d'Ohm et des mailles. Nous isolons finalement J3 en fonction de I2 et I1 pour trouver les expressions des résistances nécessaires pour que les circuits soient équivalents. Pour trouver l'expression de R3, nous échangeons les rôles des résistances en utilisant le point de symétrie du circuit. Au final, nous avons obtenu une équivalence de circuit utile en physique.

Point de fonctionnement d'une photodiode

Dans cette vidéo, Matisse de Studio explique comment déterminer le point de fonctionnement d'une photodiode, qui est un récepteur de lumière fonctionnant comme une diode. Il explique que la caractéristique courant-tension de la photodiode est tracée en mesurant l'éclairage avec une lampe halogène et en la montant en série avec une résistance de 10 000 ohm. Pour trouver le point de fonctionnement, on doit superposer cette courbe avec celle imposée par le circuit, dont la loi de U est déterminée par la loi d'Ohm. En utilisant deux points, on peut déterminer la droite représentant la courbe, et donc le point de fonctionnement, qui est de moins 0,28 mA. Cela permet de connaître la tension et l'intensité du circuit.

Pont de Wheatstone

Dans ce cours sur le pont de Wheatstone, Matisse de Studio présente un circuit composé d'un générateur de courant continu et de quatre résistances. Il explique comment déterminer les tensions UBC, UDC et UAC et que UAC équivaut à E en utilisant la loi d'Ohm. En supposant que l'intensité du courant dans le voltmètre est quasi nulle, il identifie les valeurs de UBC et UDC en utilisant le diviseur de tension. En déduisant la tension UDB mesurée par le voltmètre, il donne une formule pour calculer la résistance R en fonction des résistances R1, R2 et R3 du pont de Wheatstone. Enfin, il explique comment utiliser le pont de Wheatstone pour déterminer une résistance inconnue en équilibrant le pont et en annulant la tension UDB.

Théorème de Millman

Dans cette vidéo, Matisse de Studio explique une application concrète du théorème de Millman. Il étudie un circuit électrique comprenant plusieurs résistances et un nœud central appelé M. En utilisant la loi des nœuds et la loi d'Ohm, il prouve que le potentiel en M peut être exprimé en fonction des potentiels des autres nœuds et des résistances du circuit. En développant cette équation, il obtient le célèbre théorème de Millman qui permet de calculer le potentiel en un nœud central en fonction des potentiels des autres nœuds et de leurs résistances respectives. Cette application montre que ce théorème est cohérent avec les lois d'association bien connues en électronique.

Bobines et resistances

Dans cette vidéo, Matisse de Studio explique comment déterminer l'équation différentielle liant la tension et le courant d'un circuit constitué de deux branches en parallèle, avec une bobine et une résistance en série dans chaque branche. Pour résoudre cette question, on peut utiliser les différentes relations entre la tension et les courants dans chaque branche, ainsi que la loi des nœuds en Ré. En manipulant ces équations avec des dérivées et des combinaisons, on peut exprimer I en fonction de U et obtenir l'équation différentielle recherchée. Malgré son caractère calculatoire, cet exercice montre l'importance de se concentrer sur les grandeurs que l'on cherche à démontrer et de manipuler les expressions pour les faire apparaître.

Circuit alimenté par deux générateurs

Bonjour à tous, dans cette vidéo, nous étudions un circuit alimenté par deux générateurs. Le circuit est composé d'un générateur de tension continue E en série avec une résistance R, et d'un autre générateur de tension E/2 en série avec une résistance R/2. Pour établir les équations différentielles, nous utilisons la loi des mailles pour chaque maille du circuit. On obtient ainsi deux relations : UC(t) = (E/2)*R*I1(t) et UC(t) + R*I2(t) = 2. En utilisant la loi des noeuds, nous obtenons une relation entre le courant I(t) traversant le condensateur, I1(t) et I2(t). En combinant toutes ces relations, nous obtenons une équation différentielle : (d^2UC/dt^2) + (3/(RC))*dUC/dt = (2/(RC))*E. Nous résolvons ensuite cette équation différentielle en trouvant la solution générale associée à l'équation homogène, puis en cherchant une solution particulière. En combinant ces solutions, nous obtenons l'expression complète de UC(t) : UC(t) = (E/3)*(2 + e^(-3t/RC)). Nous déterminons également les constantes de l'équation en utilisant les conditions initiales. Pour cela, nous utilisons le fait que le courant I2(t) était nul avant la fermeture de l'interrupteur, ce qui implique que UC(t=0-) = UC(t=0+) = E. En utilisant ces conditions, nous trouvons que UC(t=0) = E/3. Ensuite, nous déterminons le temps T1 nécessaire pour que UC(t) atteigne sa valeur finale à 1% près. Grâce à l'expression de UC(t), nous remplaçons UC(t) par sa valeur atteinte à 99% de sa valeur finale, ce qui nous permet d'isoler T1 dans l'expression. Nous trouvons ainsi que T1 = -(RC)*ln(0.02/3). Enfin, nous exprimons la puissance dissipée par effet Joule dans le circuit. En utilisant la loi d'Ohm, nous exprimons les tensions aux bornes des résistances en fonction de UC(t) et E. En remplaçant UC(t) par son expression, nous obtenons l'expression de la puissance dissipée. Nous remarquons que cette puissance tend vers E^2/(6R) lorsque t tend vers l'infini, ce qui est cohérent avec un raisonnement physique basé sur l'analyse du circuit. En résumé, cette vidéo présente l'étude d'un circuit alimenté par deux générateurs. Nous établissons les équations différentielles et résolvons l'équation pour trouver l'expression de la tension aux bornes du condensateur. Nous déterminons également le temps nécessaire pour atteindre la valeur finale de la tension, et exprimons la puissance dissipée par effet Joule dans le circuit.

Circuit RC parallèle

Dans cette vidéo, Matisse de Studio étudie un circuit RC en parallèle, dans lequel l'interrupteur K est brusquement fermé. Pour trouver l'expression de la tension U et tracer son allure, il applique la loi des mailles et normalise l'équation différentielle pour obtenir une solution générale et particulière. Il détermine une condition initiale à partir du régime permanent précédent et utilise cette information pour déterminer la constante arbitraire de sa solution. Enfin, il trace l'allure de la tension U en utilisant les informations trouvées précédemment et conclut que le condensateur ne se décharge pas totalement, restant à une tension de E sur 2.