Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Fonction Composée
Ce cours explique comment effectuer l'étude et le tableau de variation d'une fonction composée de deux autres fonctions. L'exemple étudié est la fonction E2-1 sur x². La fonction composée est de la forme h rongé de x, où g est –1 sur x² et h est l'exponentielle. Par composition, f est défini sur R*.
Pour faire le tableau de variation, les fonctions dérivées sont utilisées. g' est calculée et égale à 2 sur x³, ce qui est du même signe que x. Ainsi, g est décroissante de moins l'infini à 0 et croissante de 0 à plus l'infini. Les limites de g sont également calculées. En plus ou moins l'infini, g tend vers 0 et en 0, g tend vers moins l'infini.
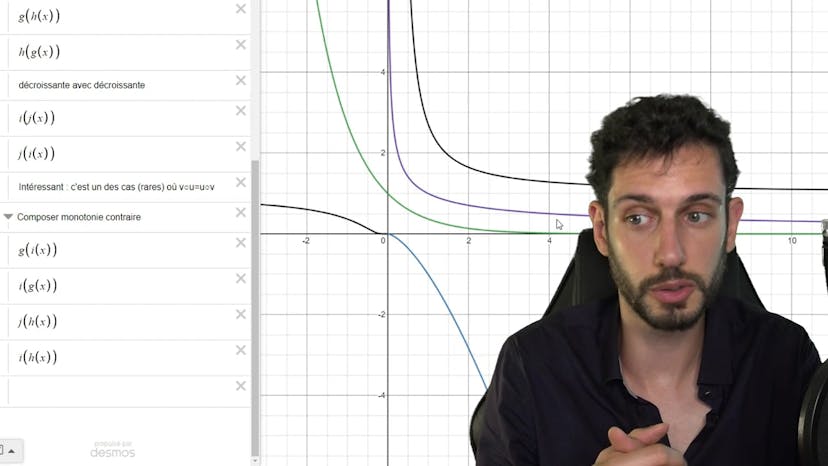
Toutes les limites sont ensuite utilisées pour construire le tableau de variation complet de g. La fonction est ensuite tracée pour observer son comportement. Il est également mentionné que si la fonction est paire, il est possible d'étudier uniquement une partie de la fonction sur un intervalle.
Ensuite, le sens de variation de la fonction composée F (H rongé de G) est étudié. La fonction exponentielle H est croissante sur R et le sens de variation de G a déjà été déterminé. Ainsi, il est déduit que F est décroissante sur R étoile moins et croissante sur R étoile plus.
Les limites de F sont calculées. En moins l'infini, G tend vers 0, et en composant avec H, F tend également vers 1. En 0, G tend vers moins l'infini, et en composant avec H, F tend vers 0. Le tableau de variation de F est ainsi obtenu, montrant qu'elle est décroissante de 1 à 0 et croissante de 0 à 1.
Enfin, il est mentionné que la fonction n'est pas définie en 0, mais on peut prolonger la fonction par continuité en posant F de 0 égale à 0. Une autre méthode aurait pu être d'étudier directement la fonction F en calculant sa dérivée.