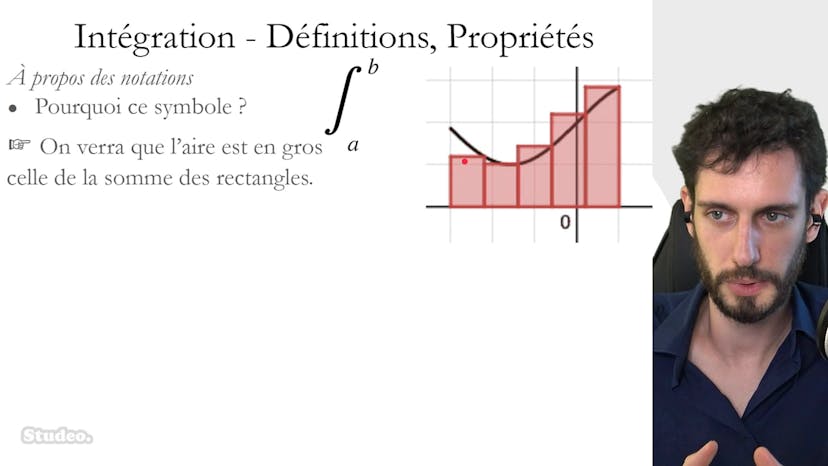
Encadrement et intuition graphique

Dans cette vidéo, nous allons explorer différentes méthodes pour approximer l'aire sous une courbe. L'objectif est de mieux comprendre le calcul de cette aire. Lorsque la courbe est une droite, le calcul de l'aire est relativement simple, en utilisant des formes géométriques telles que des triangles ou des rectangles. Cependant, dès que la courbe devient incurvée, cela se complique. Nous allons donc examiner plusieurs méthodes d'approximation, dont la méthode des rectangles supérieurs et inférieurs, qui sont les plus couramment utilisées. Avant de passer aux graphiques, examinons la définition officielle des rectangles supérieurs et inférieurs. Pour une fonction continue et positive f sur un intervalle AB, nous divisons cet intervalle en n petits intervalles de même amplitude, sur lesquels nous construisons des rectangles inférieurs et supérieurs. Les rectangles inférieurs sont situés juste en dessous de la courbe, tandis que les rectangles supérieurs sont situés juste au-dessus de la courbe. Lorsque le nombre de rectangles augmente et que leur finesse augmente également, les deux méthodes tendent vers la valeur réelle de l'aire sous la courbe. Pour illustrer ces méthodes, regardons un graphique où la fonction est croissante. La méthode des rectangles inférieurs consiste à placer plusieurs rectangles sous la courbe. Plus le nombre de subdivisions augmente, plus les rectangles deviennent fins et se rapprochent de la courbe. Ainsi, les différences entre l'aire des rectangles et l'aire réelle sous la courbe deviennent de plus en plus petites. La méthode des rectangles supérieurs consiste à placer des rectangles au-dessus de la courbe. Dans ce cas, l'aire des rectangles est légèrement supérieure à l'aire réelle sous la courbe, et est également supérieure à l'aire des rectangles inférieurs. En dehors de ces deux méthodes courantes, nous avons également mentionné la méthode du point milieu et la méthode des trapèzes. La méthode du point milieu consiste à placer des rectangles traversés par la courbe au milieu de leur côté supérieur, permettant ainsi une approximation plus précise. La méthode des trapèzes offre encore plus de liberté, car les quadrilatères utilisés ne sont plus des rectangles, mais des trapèzes. Cela permet de mieux coller à la courbe. Cette vidéo vise à aider les personnes travaillant sur le calcul d'aires et d'intégrales à mieux visualiser ces concepts. Nous espérons que cela vous a été utile. Si vous avez des questions, n'hésitez pas à les poser dans la FAQ. À bientôt dans une prochaine vidéo.