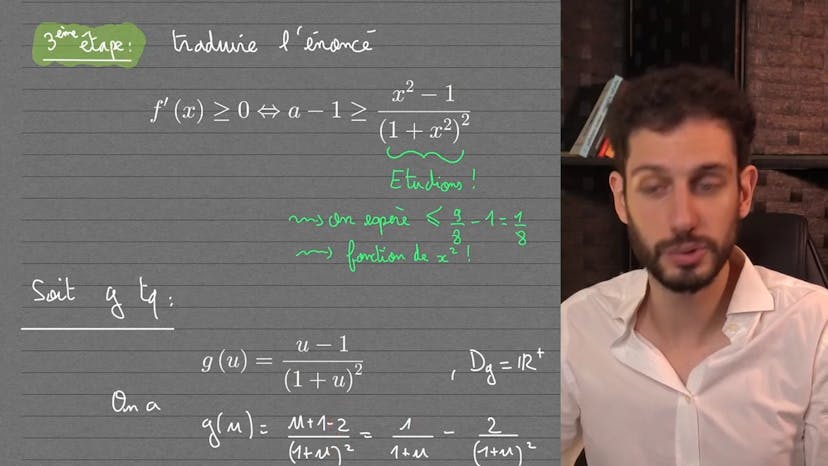Résoudre x = aˣ, et en moins de 10 minutes

Bonjour à tous ! Aujourd'hui, je vais résumer en utilisant des termes SEO-friendly un cours qui est une transcription d'une vidéo. Dans ce cours, nous allons aborder un exercice qui est tombé à Cambridge en 2014. Cet exercice ressemble à un exercice d'analyse de fonctions qui peut être réalisé en Terminale, grâce aux outils que nous utilisons régulièrement. L'énoncé nous demande de démontrer que l'équation x égale a puissance x n'a aucune racine réelle si a est strictement supérieur à e puissance 1 sur e. Nous supposons que a est positif pour simplifier les calculs. Ensuite, nous déduisons que x doit également être positif pour éviter une contradiction. Pour résoudre cette équation, nous prenons le log de chaque côté pour simplifier les calculs. En dérivant, nous étudions les variations de la fonction f et trouvons son maximum. En analysant les limites de la fonction, nous déterminons les conditions pour lesquelles elle a des racines réelles ou non. Finalement, nous concluons que si a est strictement supérieur à e puissance 1 sur e, l'équation n'a pas de racines réelles, et si a est strictement inférieur à 1, l'équation a une unique racine réelle. J'espère que cette résumé SEO-friendly vous a aidé à comprendre le contenu du cours. N'hésitez pas à vous abonner à la chaîne pour plus de vidéos et de conseils mathématiques. À bientôt !