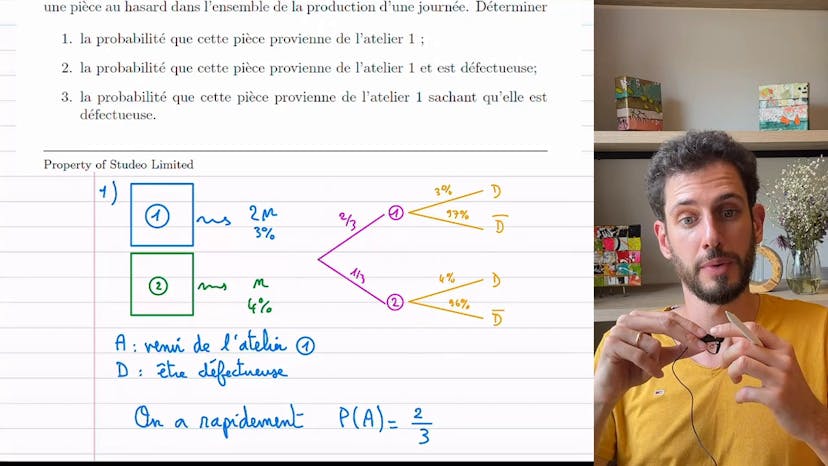
Formule de Bayes

On a un gérant de magasin d'informatique qui a reçu un lot de clés USB. 5% des boîtes sont abîmées. Le gérant estime que 60% des boîtes abîmées contiennent au moins une clé défectueuse. 98% des boîtes non abîmées ne contiennent aucune clé défectueuse. Un client achète une boîte du lot. On cherche à calculer les probabilités suivantes : P(A), P(~A), P(D|A), P(D|~A), P(~D|A), P(~D|~A), et P(D). En utilisant la formule des probabilités totales, on obtient P(D) = 4,9%. Si un client constate qu'une clé achetée est défectueuse, la probabilité qu'il ait acheté une boîte abîmée est de 61,2%. Il y a donc 40% de chances qu'une clé défectueuse provienne d'une boîte non abîmée.