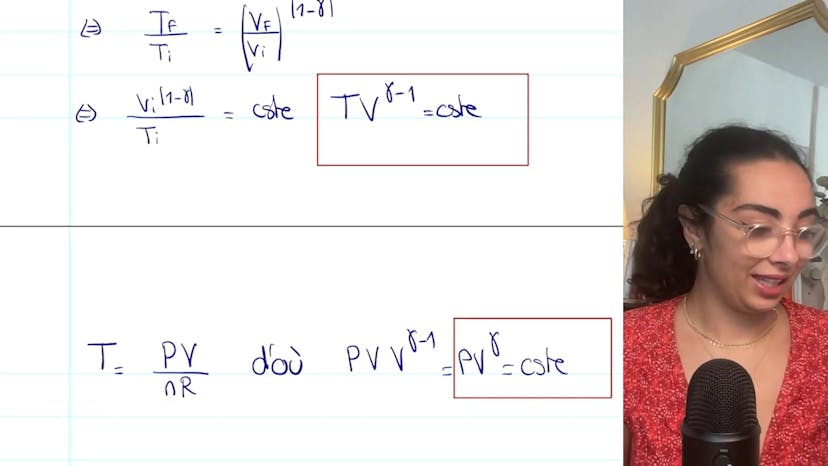Variation d'entropie pour gaz parfait

Aujourd'hui, nous allons étudier la variation d'entropie pour un gaz parfait. La première identité thermodynamique est une formule essentielle pour calculer cette variation. Elle relie les différentiels des différentes grandeurs thermodynamiques telles que U, S, T, P et V. Nous pouvons isoler le terme DS dans cette formule en écrivant DS = DU/T + PDV/T. Comme nous savons que la variation d'énergie interne (DU) dépend uniquement de la température (T), nous pouvons la remplacer par CVDT/T, où CV est la chaleur spécifique à volume constant. Nous pouvons simplement intégrer la température entre la température initiale et la température finale. Le terme restant dans cette formule contient les variables P, V et T. Pour simplifier l'intégrale, nous pouvons utiliser la loi des gaz parfaits (PV = NRT), ce qui nous donne P/T = NR/V. Ainsi, nous avons seulement NRDV/V dans cette intégrale, ce qui correspond à une intégrale d'une seule variable. Finalement, nous intégrons cette formule pour passer de DS à delta S (variation de l'entropie). Comme S est une fonction d'état, nous pouvons utiliser le symbole delta. Ainsi, nous obtenons NCVM ln(TF/TI) + NR ln(VF/V), où NCVM est le produit du nombre de moles (N) et de la chaleur spécifique molaire à volume constant (CV), et TF, TI, VF et V sont les températures et volumes initiaux et finaux respectivement. Cette formule peut être écrite de différentes manières en fonction des grandeurs données dans l'exercice. Par exemple, on peut utiliser la masse molaire pour exprimer la variation d'entropie de manière massique, ou substituer CV par CP (chaleur spécifique à pression constante). Notez également qu'il est possible de conserver d'autres grandeurs thermodynamiques dans la formule, telles que la pression (P). Ainsi, la variation d'entropie peut être exprimée en fonction d'autres paires de grandeurs, telles que TV ou TP. En résumé, il est important de connaître la première identité thermodynamique pour calculer la variation d'entropie d'un gaz parfait. Cette formule peut être adaptée en fonction des grandeurs disponibles dans l'exercice, mais il est recommandé de la réduire à une forme plus simple avant d'effectuer les calculs.