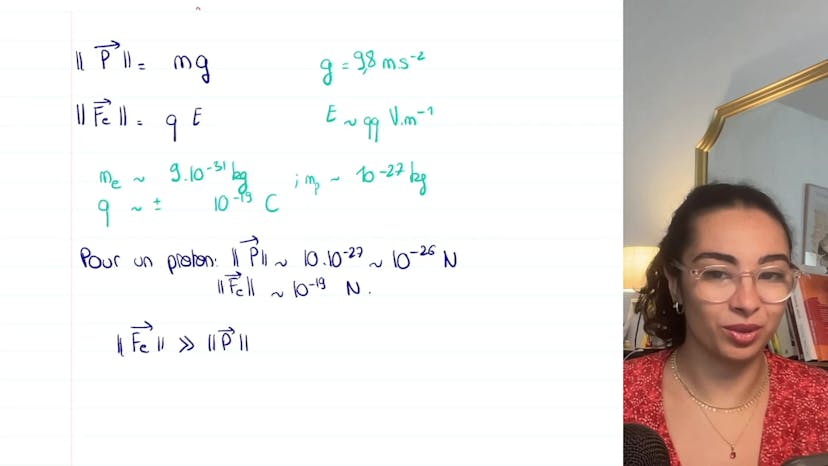Champ électrique inconnu

Dans ce cours, nous nous intéressons à un champ électrique inconnu et à la déviation d'une particule à travers ce champ. L'exercice consiste à déterminer la norme du champ électrique et l'angle de déviation de la trajectoire. Pour commencer, nous devons déterminer la direction du champ électrique statique U0. On sait que le champ électrique tend à accélérer les électrons en changeant leur trajectoire. Donc, l'électron est dévié vers le haut, ce qui signifie que la force électrique le pousse vers le haut (UY). Étant donné que l'électron a une charge négative, la force électrique est opposée au champ électrique, ce qui implique que E est opposé à UY. Ensuite, nous devons déterminer le signe de la variation de l'énergie cinétique (ΔEC), c'est-à-dire si elle augmente ou diminue. Comme la vitesse de la particule est toujours positive le long de la trajectoire, la puissance apportée par la force électrique est positive, ce qui signifie que la différence d'énergie cinétique est également positive. Maintenant, nous devons trouver la norme de E0. Pour cela, nous utilisons le travail de la force électrique entre l'entrée et la sortie du champ, qui est égal à moins E fois E0 fois la distance ES (delta Y). En utilisant la ligne droite entre E et S pour simplifier notre calcul, nous obtenons E times E0 times delta Y. En appliquant le principe fondamental de la dynamique, on trouve les équations horaires du mouvement de la particule. En éliminant le temps, on peut écrire l'équation de la trajectoire en fonction de la position horizontale X. En utilisant la distance L pour X, on obtient une équation reliant E0, L, M et V0. Enfin, nous pouvons déterminer l'angle de déviation de la trajectoire en utilisant la vitesse en Y et la vitesse en X à la sortie du champ. En remplaçant les valeurs avec celles obtenues précédemment, nous trouvons que l'angle de déviation tan alpha est égal à E0L/MV0^2. En utilisant la valeur de l'énergie cinétique obtenue précédemment, nous pouvons calculer cet angle. En résumé, l'exercice consiste à déterminer la norme du champ électrique E0 qui dévie une particule à travers une certaine distance L dans un champ électrique constant. Nous avons également calculé la direction du champ électrique, le signe de la variation de l'énergie cinétique et l'angle de déviation de la trajectoire en fonction des grandeurs données.