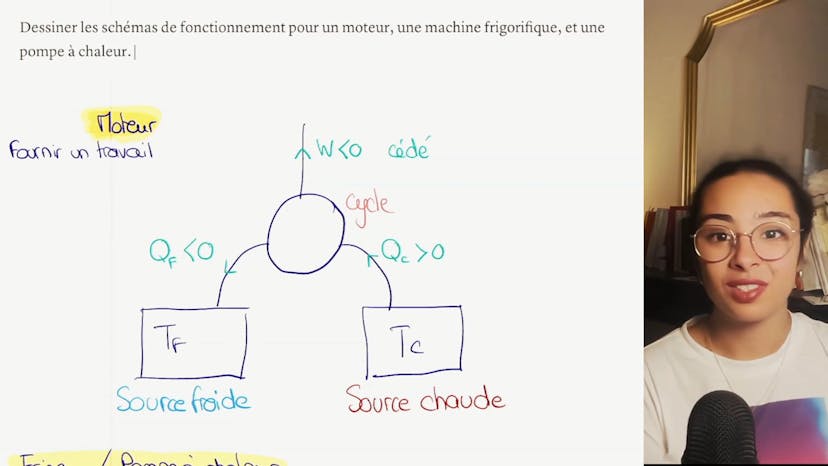
Efficacités et rendements

Dans ce cours, on apprend à calculer les efficacités et les rendements des machines thermiques. L'efficacité ou le rendement est défini comme l'énergie utile divisée par l'énergie consommée. Pour un moteur, le rendement est égal à l'énergie utile (W) divisée par l'énergie consommée (QC), et il est toujours inférieur à 1. On utilise les principes du second principe et du cycle de fonctionnement pour éliminer le travail (W) et obtenir l'efficacité en fonction de QF (énergie cédée) et QC (énergie consommée). On peut aussi faire le lien avec les températures en utilisant l'inégalité de Clausius. L'efficacité est donc inférieure à 1-TF/TC, où TF et TC sont les températures respectives de la source froide et de la source chaude. Cette valeur est appelée le rendement de Carnot, qui représente le meilleur rendement possible. Dans le cas d'une pompe à chaleur, on utilise le même procédé pour calculer l'efficacité, qui est égale à moins QC sur W. En utilisant les principes et l'inégalité de Clajus, on trouve que l'efficacité est inférieure à 1- TF/TC. Ces calculs sont importants pour comprendre le fonctionnement des machines thermiques et peuvent être appliqués à des machines plus complexes.