Hydrolyse du saccharose

Dans cette vidéo, nous étudions l'hydrolyse du saccharose. Le saccharose se décompose en glucose et en fructose dans l'eau. La réaction est la suivante : C12H22O11 + H2O donne C6H12O6 + C6H12O6. Le glucose et le fructose sont des isomères, ce qui signifie qu'ils ont la même formule brute. Nous observons l'évolution temporelle de la concentration en saccharose dans une solution. La concentration est exprimée en millimoles par litre et le temps en minutes. Il est important de bien repérer les unités pour éviter les erreurs dans les résultats. 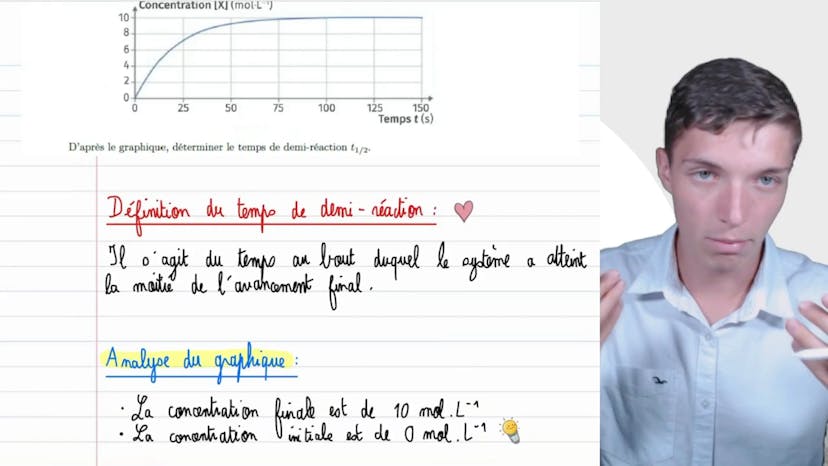La première question consiste à tracer la courbe de concentration en fonction du temps. Pour cela, nous utilisons un tableau et le logiciel de régression si disponible. Ensuite, nous déterminons graphiquement les vitesses volumiques de disparition du saccharose aux instants 0, 300, 600 et 900 minutes. La vitesse volumique de disparition correspond à la pente de la tangente à la courbe de concentration en fonction du temps. Elle est positive car il s'agit d'une vitesse de disparition. Les vitesses volumiques de disparition obtenues sont les suivantes : V1 = 0,6 mmol/L/min, V2 = 0,3 mmol/L/min, V3 = 0,1 mmol/L/min, et V4 = 0,05 mmol/L/min. Ensuite, nous traçons les différentes vitesses en fonction de la concentration. Mis à part la dernière mesure qui fausse légèrement les résultats, nous obtenons une droite caractéristique d'une cinétique d'ordre 1. Cela signifie que la vitesse est proportionnelle à la concentration, conformément à l'équation V = k * c. Cette conclusion est également cohérente avec le temps de demi-vie de la réaction, qui est indépendant de la concentration initiale en réactif. Dans une réaction d'ordre 1, le temps de demi-réaction est égal à ln(2)/k et ne dépend pas de la concentration initiale. En conclusion, l'ordre de la réaction par rapport au saccharose est de 1. Il est recommandé de revoir la méthode si vous n'avez pas encore assimilé cette configuration classique de détermination de l'ordre de réaction. Merci d'avoir suivi cette vidéo. À bientôt !