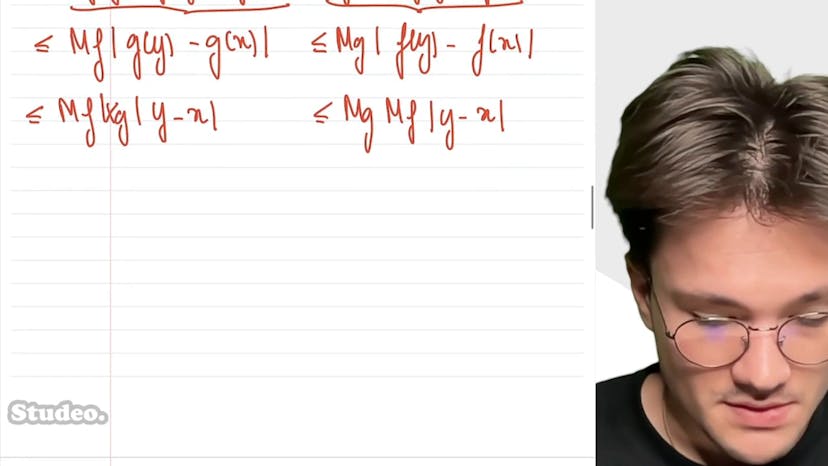Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Logique et ensembles
- Calcul algébrique et trigonométrie
- Complexes
- Fonctions d'une variable réelle (0)
- Primitives et équations différentielles
- Nombres réels et suites numériques
- Fonctions : Limites et continuité (1)
- Fonctions : dérivabilité (2)
- Fonctions : convexité (3)
- Analyse Asymptotique
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Logique et ensembles
- Calcul algébrique et trigonométrie
- Complexes
- Fonctions d'une variable réelle (0)
- Primitives et équations différentielles
- Nombres réels et suites numériques
- Fonctions : Limites et continuité (1)
- Fonctions : dérivabilité (2)
- Fonctions : convexité (3)
- Analyse Asymptotique
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Type Mines : Partie A - 2/4
Ce cours traite de la démonstration de l'existence de deux réels positifs a et b pour toute fonction Lipschitzienne f, telle que pour tout réel x, la valeur absolue de f de x soit inférieure ou égale à a fois la valeur absolue de x plus b. La démonstration repose sur une inégalité triangulaire et sur le caractère Lipschitzien de f. Ensuite, le cours aborde la question de la généralisation de cette propriété pour toutes les fonctions vérifiant que pour tout réel x et y, ayant une distance inférieure ou égale à 1, on a f de y moins f de x inférieur ou égal à m fois y moins x. Pour cela, il est nécessaire de montrer que la fonction en question appartient à l'ensemble des fonctions Lipschitzienne. La démonstration passe par une décomposition et une majoration de la différence de f entre deux réels x et y, d'une distance strictement supérieure à 1, en utilisant une combinaison télescopique et l'inégalité triangulaire. Finalement, la propriété Lipschitzienne est établie, et la fonction est montrée comme étant m-lipschitzienne.