Vitesse et accélération

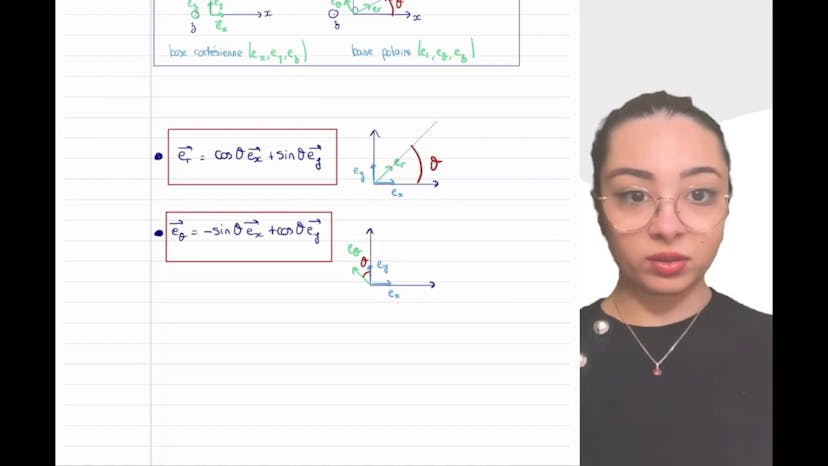
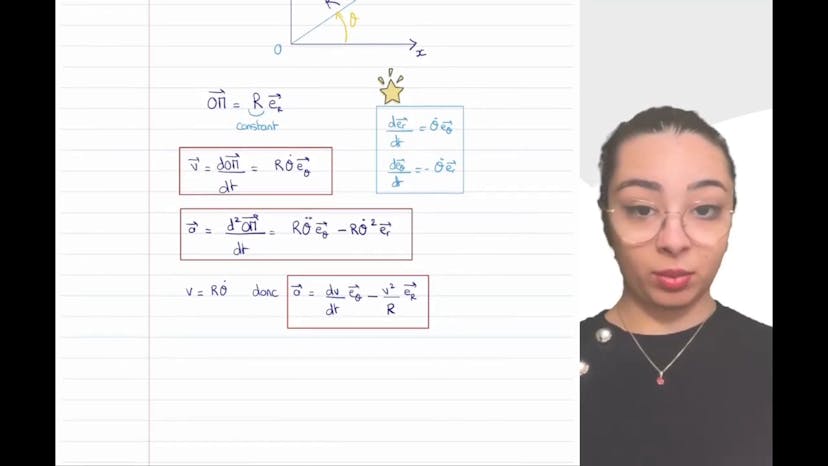
Dans ce cours, Leïla explique comment exprimer la vitesse et l'accélération d'un point en coordonnées cylindriques. Elle utilise la formule OM = RER + ZEZ pour déterminer le vecteur déplacement. Elle note que ER change en fonction de la base, mais EZ est fixe. Elle mentionne également la formule DER/Dt = θ.eθ et DET/Dt = -θ.er pour dériver les vecteurs mobiles par rapport au temps. Pour la vitesse, elle dérive le vecteur position par rapport au temps et applique la formule DER/Dt = θ.eθ pour obtenir l'expression de la vitesse en coordonnées cylindriques R.ERθ.ez. Pour l'accélération, elle dérive la vitesse et applique la formule des produits de trois termes pour obtenir l'expression de l'accélération en coordonnées cylindriques. Elle insiste sur l'importance de connaître cette formule pour résoudre les problèmes de mécanique en base cylindrique.