Pression nul

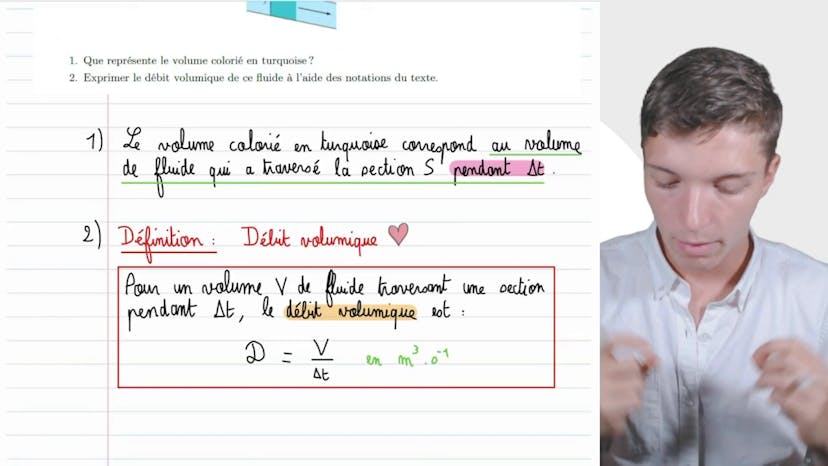
Dans cette vidéo, Matisse de Studio aborde le problème des cas particuliers où la pression s'annule dans un écoulement, ce qui peut provoquer la formation de bulles et perturber le débit. Il commence par rappeler la loi de Bernoulli et la relation de conservation du débit. En utilisant ces équations, il exprime la pression P1 en fonction des autres paramètres. En simplifiant les termes, il obtient l'équation suivante : V02/2 + P0/ρ = V12/2 + P1/ρ. Ensuite, en utilisant la conservation du débit (D = V * S), il montre que V1 peut être exprimée en fonction de V0 et des différentes sections (S0 et S1). En simplifiant cette équation, il obtient V1 = V0 * S0/S1. Il utilise ensuite cette expression pour réécrire l'équation de Bernoulli en fonction de V0, S0, S1, P0 et P1. Après simplification, il obtient V02/2 + P0/ρ = V02*S0²/S1² + P1/ρ. Il poursuit en supposant que la pression P1 s'annule, ce qui permet de supprimer ce terme dans l'équation. En inversant les termes, il obtient finalement une expression pour la vitesse V0 à partir de laquelle la pression P1 s'annule : V0 = √(P0/(2ρ * (S0²/S1² - 1))). En résumé, cette vidéo aborde le problème des cas où la pression s'annule dans un écoulement. En utilisant la loi de Bernoulli et la relation de conservation du débit, Matisse parvient à exprimer la pression P1 en fonction des autres paramètres. Il montre ensuite comment calculer la vitesse à partir de laquelle la pression P1 s'annule.