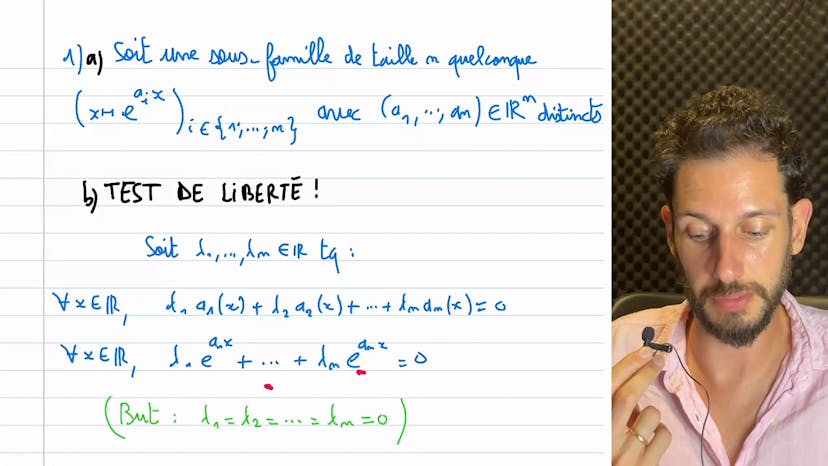Encore des familles de fonctions

Le cours porte sur la question de savoir si une famille de fonctions est libre ou non. Dans la question 1, on nous donne trois fonctions sinus différentes et on nous demande de montrer si elles sont liées. Tout d'abord, on utilise quelques formules trigonométriques pour exprimer ces fonctions uniquement en fonction de sinus. Ensuite, on montre que deux des fonctions sont liées à sinus x et on fait la même démarche avec la troisième fonction pour obtenir une relation entre les trois fonctions. Ainsi, on conclut que la famille est liée. Dans la question 2, on nous donne une famille de fonctions qui sont des polynômes de degré 1. Au début, l'auteur se perd un peu dans ses calculs, mais réalise finalement que toutes ces fonctions sont en fait des combinaisons linéaires d'une constante et de x. Donc, quel que soit l'élément de la famille, on peut l'exprimer comme une combinaison linéaire des deux premiers éléments de la famille. Donc, toute sous-famille de cette famille est également liée, ce qui signifie que la famille entière est liée. En conclusion, le cours traite de la question de la liberté d'une famille de fonctions. Dans les deux questions abordées, on montre que les familles sont liées, ce qui signifie qu'elles ne sont pas libres. L'auteur souligne également l'importance de prendre du recul et de comprendre les structures mathématiques pour résoudre efficacement ce type d'exercice.