Cours de Logique et ensembles en Ligne par les Meilleurs Professeurs - Logique et ensembles

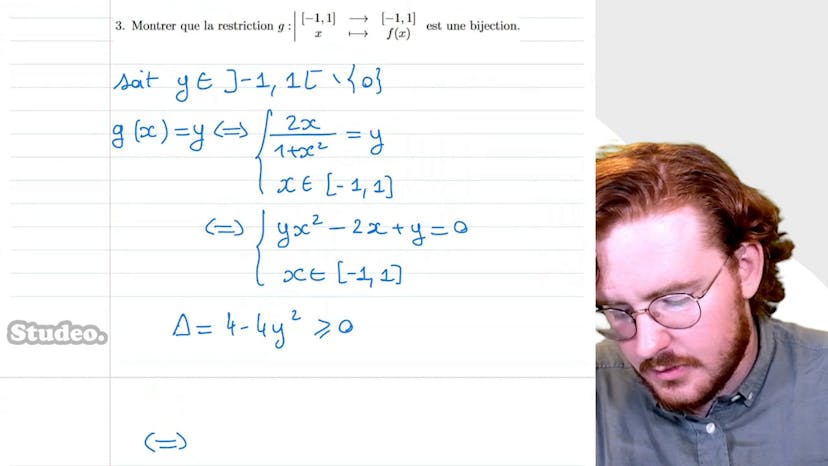
Injection, surjection : exemple

Dans cette vidéo sur les fonctions à variable réelle, Paul explore l'injectivité, la surjectivité et la bijectivité. Il prend une fonction f définie par 2r dans R, avec f(x) = 2x/(1+x^2). Paul utilise le graphique de f pour montrer que f n'est pas injective car f(1.5) = 4.5 et f(2) = 4.5. Il calcule ensuite le delta de l'équation f(x) = 2 degré, ce qui montre que f n'est pas surjective non plus.Paul prouve ensuite que l'image de f est le segment [-1,1], ce qui montre que f est surjective lorsqu'elle est restreinte à cet intervalle. Enfin, il montre que la restriction de f à l'intervalle [-1,1] est bijective en trouvant des expressions pour la solution unique à l'équation g(x) = y.

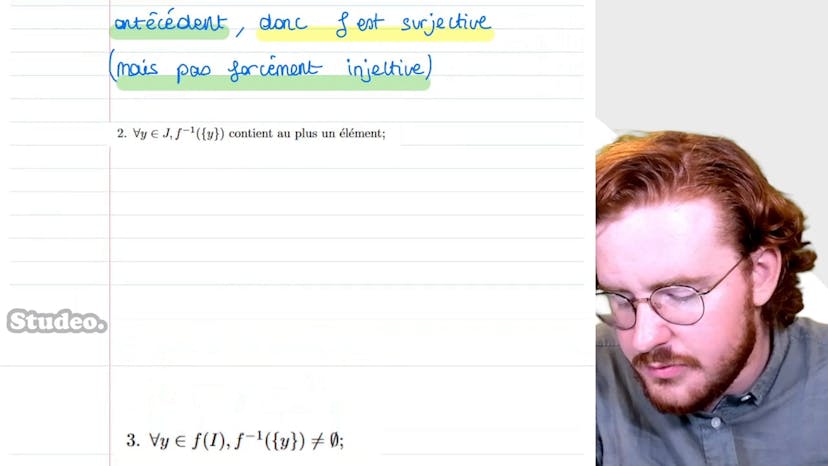
Injection, surjection : propriétés

Le cours traite des notions d'injectivité, de surjectivité et de bijection dans les applications mathématiques. Il énonce quatre propriétés permettant de déterminer si une fonction est injective, surjective ou bijective, ou si aucun de ces termes ne s'applique. Pour résumer, l'injectivité signifie qu'un élément de l'ensemble d'arrivée admet au plus un antécédent, la surjectivité signifie que tout élément de l'ensemble d'arrivée a au moins un antécédent et la bijection combine ces deux propriétés en affirmant que chaque élément de l'ensemble d'arrivée a un unique antécédent. Les propriétés énoncées permettent également de déduire qu'une fonction peut être surjective mais pas injective, injective mais pas surjective, bijective ou ne répondre à aucune de ces catégories.

Ensembles images

Dans cette vidéo, Paul parle de la manipulation d'images entre deux ensembles, E et F, et explique comment démontrer que A est inclus dans B en implique F de A inclus dans F de B. Il montre également que l'inclusion réciproque n'est pas toujours vraie. Ensuite, il démontre que F de A inter B est inclus dans F de A intersection F de B, mais que l'inclusion réciproque n'est pas toujours vraie. Enfin, il explique que l'image de l'union d'un ensemble est égale à l'union des images de cet ensemble, mais que cela n'est vrai que dans un sens pour l'intersection.

Relation d'équivalence

Dans cette vidéo, on explore la relation d'équivalence R définie pour les ensembles des réels où X est en relation avec Y si X exponentielle de Y est égale à Y exponentielle de X. Pour montrer qu'une relation est une relation d'équivalence, il faut démontrer que la relation est réflexive, symétrique et transitive, tout comme l'égalité. La relation R est donc une relation d'équivalence.Ensuite, la question 2 demande de préciser, pour chaque réel X, le nombre d'éléments dans la classe d'équivalence de X (c'est-à-dire, combien de réels sont en relation avec X selon R). On introduit la fonction T(t) = t exponentielle de -t et on note C2x la classe d'équivalence pour X. En réarrangeant l'énoncé de la relation R, on trouve que C2x est l'ensemble Y tel que F2x égale F2y où F(t) = t exponentielle de -t.Pour trouver les antécédents de F2x (c'est-à-dire, les réels en R qui sont en relation avec X selon R), on étudie le graphe de F, qui est dérivable, et on remarque qu'il y a deux parties, X supérieur à 0 et X inférieur ou égal à 0. Pour X supérieur à 0, la classe d'équivalence a deux éléments, et pour X inférieur ou égal à 0, la classe d'équivalence a un élément. Ainsi, le nombre d'éléments dans la classe d'équivalence de X dépend du signe de X.

On redéfinit l'injectivité

Dans cette vidéo, on parle de la preuve de l'équivalence entre deux propositions P1 et P2, où P2 est l'injectivité de la fonction f. La question est de trouver la négation des deux propositions avec des quantificateurs, pour prouver que non P1 est équivalent à non P2. Pour cela, il est conseillé de traduire les propositions en français avant de les traduire en quantificateurs et de prendre la négation. Ensuite, la video nous guide à travers les étapes pour prouver les deux sens de cette équivalence, en utilisant la négation des propositions. Finalement, la preuve montre que P1 et P2 sont équivalentes.

Bijection dans N

Dans cette vidéo, Paul aborde l'exercice sur la bijectivité et montre comment démontrer qu'une fonction est bijective. Il explique que pour prouver l'injectivité, il faut trouver des relations entre les nombres entiers, les diviseurs, et les nombres pairs et impairs. Pour prouver la surjectivité, il faut décomposer un nombre en facteurs premiers et trouver l'existence de son antécédent. À partir de là, il montre comment composer f avec une bijection de n étoiles dans n pour obtenir une bijection de n² dans n, en utilisant une application simple qui associe n à n-1. En résumé, l'exercice consiste à prouver la bijectivité d'une fonction et à trouver une bijection de n² dans n.

Mathématiques