Essai gratuit

Tous les sujets

Terminale

Première

Seconde

MPSI/PCSI

2BAC SM Maroc

Level

Tous les sujets

Terminale

Première

Seconde

MPSI/PCSI

2BAC SM Maroc

Level

Corrigés de BAC

Bac Physique-Chimie

Terminale

Observation de la planète Mars (1)

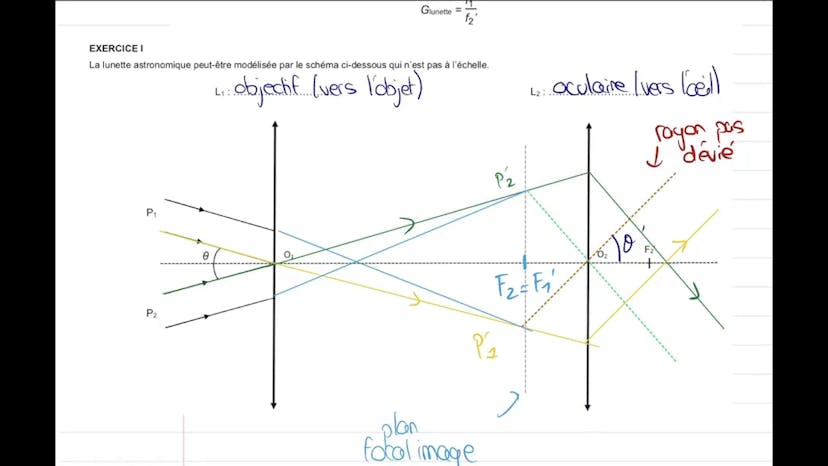
Dans cette vidéo, nous nous intéressons à l'exercice 1 d'un sujet sur l'observation de la planète Mars. Cet exercice porte sur l'optique d'une lunette astronomique en utilisant des rayons lumineux. Tout d'abord, nous devons identifier sur le schéma les lentilles qui jouent le rôle de l'objectif et de l'oculaire. Ensuite, nous apprenons que la lunette astronomique est affocale, ce qui signifie qu'elle renvoie une image à l'infini d'un objet situé à l'infini. Cela permet de ne pas fatiguer les muscles des yeux. Nous devons également tracer les rayons lumineux et expliquer pourquoi l'observateur ne voit qu'un point lumineux lorsqu'il regarde Mars à l'œil nu. Cela est dû au pouvoir de résolution de l'œil, qui détermine l'angle au-delà duquel l'œil distingue deux points séparés. Si cet angle est plus petit que l'angle de vision de l'observateur, il ne pourra pas distinguer les deux points. En utilisant la lunette astronomique, l'observateur voit un disque lumineux où il peut distinguer le haut et le bas de Mars. Cela est dû au grossissement de la lunette, qui permet de mieux résoudre le système. En résumé, cet exercice aborde l'utilisation de la lunette astronomique pour observer la planète Mars, en se concentrant sur l'optique et le pouvoir de résolution de l'œil.

Corrigés de BAC

Bac Physique-Chimie

Terminale

Observation de la planète Mars (2)

Dans cette vidéo, Laila de STUDIO explique comment déterminer le diamètre de la planète Mars à partir des mesures d'angle obtenues à travers une lunette astronomique. Elle commence par présenter les données disponibles, telles que les angles θ1 et θ2 mesurés aux points A et B, ainsi que la distance Soleil-Mars. En analysant le schéma, elle déduit que θ1 correspond à θA et θ2 correspond à θB, puis elle utilise la trigonométrie pour établir l'expression du diamètre dm de Mars en fonction de θA et θB. Dans la figure 2, elle observe que la distance D1 + D2 est égale à deux fois la distance Soleil-Mars, ce qui lui permet d'exprimer dm en fonction de cette distance. En effectuant un calcul numérique, elle trouve que le diamètre de Mars est de 6,8 x 10^3 km. Cette valeur est proche du diamètre moyen de référence, ce qui confirme l'efficacité de la méthode utilisée. Elle conclut en indiquant qu'elle abordera la dernière partie de l'exercice dans une prochaine vidéo.

Corrigés de BAC

Bac Physique-Chimie

Terminale

Observation de la planète Mars (3)

Aujourd'hui, Layla de STUDIO termine l'exercice 1 du sujet de bac sur l'observation de la planète Mars. Les deux premières parties ont porté sur l'étude de Mars du point de vue optique, en utilisant une lunette astronomique pour déduire son diamètre. Dans cette dernière partie, on passe à la mécanique et on cherche à déterminer la masse de Mars en observant le satellite Phobos et en utilisant les lois de Newton. Le satellite est soumis uniquement à la gravité de Mars. Pour déterminer la vitesse de Phobos sur son orbite circulaire, on utilise la seconde loi de Newton et le repère de Freinet. Grâce à la formule de l'accélération dans ce repère, on trouve que la vitesse de Phobos est égale à la racine de gm/rmp, où gm est la constante gravitationnelle de Mars et rmp le rayon de l'orbite de Phobos. Ensuite, pour déterminer la masse de Mars, on utilise une méthode ouverte. On peut utiliser les valeurs connues de la période de révolution de Phobos et du rayon de son orbite, ainsi que la relation entre la vitesse et la masse de Mars que l'on vient de trouver. En résolvant les équations, on trouve que la masse de Mars est d'environ 464 fois 10^23 kg, ce qui est cohérent avec l'information donnée selon laquelle la masse de Mars est environ dix fois moins grande que celle de la Terre.

Corrigés de BAC

Bac Physique-Chimie

MPSI/PCSI

Observation de la planète Mars (1)

Leïla de Studio présente le premier exercice d'un sujet tombé l'année dernière en métropole portant sur l'observation de la planète Mars. Cet exercice est noté sur 10 points et concerne la physique. Dans cette introduction, Leïla introduit le sujet en expliquant qu'on souhaite évaluer les caractéristiques de Mars. Elle présente également les formules générales et les valeurs numériques qui seront utilisées tout au long de l'exercice. Dans la première partie de l'exercice, on s'intéresse à l'observation de Mars avec une lunette astronomique. Leïla explique comment différencier l'objectif de l'oculaire sur le schéma fourni. Elle souligne également que la lunette astronomique est affocale, ce qui signifie qu'elle renvoie une image à l'infini d'un objet situé à l'infini. Cela évite la fatigue des yeux. Pour cela, il faut que F2 soit égal à F1'. Ensuite, il est demandé de tracer les marges des rayons lumineux. Leïla explique qu'il faut tracer des rayons importants, notamment ceux qui passent par le centre des lentilles. Elle montre comment tracer ces rayons et souligne que les autres rayons peuvent suivre le même principe. Le calcul du grossissement de la lunette utilisée est demandé. Leïla montre la formule à utiliser et fait l'application numérique pour trouver un grossissement de 45. Enfin, il est demandé de justifier l'observation d'un observateur qui regarde Mars à l'œil nu et qui voit un point lumineux. Leïla explique que cela s'explique par le fait que l'angle de vision de l'observateur est inférieur à l'angle de résolution de l'œil, ce qui fait que les deux rayons lumineux provenant du sommet et du bas de Mars convergent sur la même cellule de la rétine, donnant l'impression d'un point unique. En utilisant la lunette astronomique, l'observateur voit un disque car le grossissement permet de distinguer les deux points de la planète Mars. Leïla fait le calcul pour trouver l'angle de vision à travers la lunette. En conclusion, Leïla espère que cet exercice aura été utile et annonce la suite du sujet.

Corrigés de BAC

Bac Physique-Chimie

MPSI/PCSI

Observation de la planète Mars (2)

Dans cet exercice, nous avons étudié la façon de déterminer le diamètre de la planète Mars en utilisant des mesures d'angle effectuées à travers une lunette astronomique. Nous avons commencé par identifier les angles θ1 et θ2 sous lesquels Mars est observée depuis les points A et B. En utilisant la figure 2, nous avons montré que le diamètre de Mars, dm, s'exprime par la formule θA = dm/D. Nous avons également noté que le diamètre de Mars peut être exprimé en fonction de grandes distances, grand D1 et grand D2, qui sont deux fois la distance Soleil-Mars. En effectuant des calculs numériques, nous avons obtenu une valeur de dm égale à 6,8 × 10^3 km, qui est proche du diamètre moyen de référence. Cette méthode s'est donc avérée efficace pour déterminer le diamètre de Mars.

Corrigés de BAC

Bac Physique-Chimie

MPSI/PCSI

Observation de la planète Mars (3)

Dans cette vidéo, nous terminons l'exercice 1 du sujet de bac qui porte sur l'observation de la planète Mars. Les deux premières parties de cet exercice ont porté sur l'étude de Mars du point de vue optique. Nous avons utilisé la lunette astronomique pour déduire le diamètre de Mars. Dans cette dernière partie, nous nous intéressons à la masse de Mars en utilisant les lois de Newton. Nous assimilons Mars à une sphère de diamètre dm et de masse M, environ dix fois plus petite que celle de la Terre. Pour déterminer cette masse, nous observons le satellite naturel de Mars, Phobos, et utilisons les lois de Newton. Nous connaissons la période de révolution de Phobos, sa trajectoire et le fait qu'il est soumis uniquement à la force de gravitation de Mars. Pour déterminer la vitesse de Phobos sur son orbite circulaire, nous utilisons la deuxième loi de Newton avec un bilan des forces. Nous utilisons le système Phobos dans le référentiel centré sur la masse de Mars et faisons un bilan des forces. Nous déduisons que la force gravitationnelle est égale à la masse multipliée par l'accélération. Nous utilisons ensuite la formule de l'accélération dans le repère de Freinet pour les mouvements de planètes circulaires, qui nous permet d'exprimer l'accélération en fonction de la vitesse et du rayon de l'orbite. En isolant la vitesse, nous obtenons l'égalité v²/rmp = gm/rmp², où g est la constante de gravitation et mm est la masse de Mars. Pour déterminer la masse de Mars, nous devons prendre des initiatives et présenter notre méthode. Nous connaissons la période de révolution de Phobos et le rayon de son orbite. Nous avons également établi une relation entre la vitesse et la masse de Mars. Nous utilisons la propriété d'une orbite circulaire pour établir le lien entre la vitesse, la période et le rayon. En égalant les deux expressions de la vitesse obtenues précédemment, nous pouvons isoler la masse de Mars. En résolvant numériquement, nous obtenons une valeur de 464 x 10^23 kg, environ dix fois plus grande que la masse de la Terre, ce qui est cohérent. En conclusion, cet exercice nous a permis d'utiliser les lois de Newton pour déterminer la masse de la planète Mars en observant son satellite Phobos.