Cours de Ondes et signaux en Ligne par les Meilleurs Professeurs - Ondes et signaux

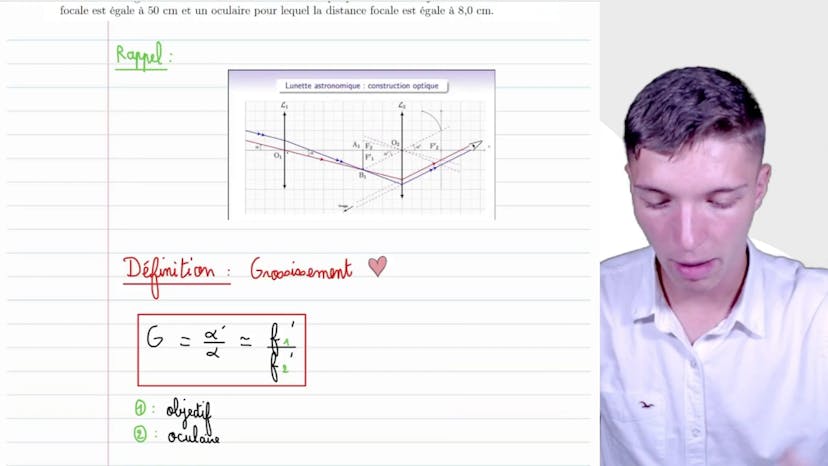
Grossissement

Dans cette vidéo, on aborde le sujet de la lunette astronomique et on se concentre sur le calcul du grossissement. Pour cela, on nous donne les valeurs de la distance focale de l'objectif (50 cm) et de l'oculaire (8 cm). Avant de passer au calcul, on présente brièvement la lunette astronomique. Elle est composée d'un objectif, qui est la première lentille convergente rencontrée par les rayons lumineux, et d'un oculaire, qui est la deuxième lentille convergente permettant de faire converger les rayons vers l'œil de l'observateur. Le foyer F2 de l'oculaire est confondu avec le foyer image F1 de l'objectif, ce qui rend le montage afocal. En ce qui concerne le calcul du grossissement, on utilise la formule classique : le grossissement est égal à l'angle alpha prime sous lequel on observe les rayons sortant de l'oculaire, divisé par l'angle alpha incident des rayons par rapport à l'axe optique arrivant sur l'objectif. Cependant, cette formule peut être approximée pour des angles très petits et équivaut à F1' / F2'. F1' représente la distance focale de l'objectif et F2' représente la distance focale de l'oculaire. Le grossissement est donc égal à F1' / F2'. Dans cet exercice, le grossissement est de 6,3. En conclusion, on a ainsi calculé le grossissement d'une lunette astronomique en utilisant les valeurs des distances focales de l'objectif et de l'oculaire. Le grossissement est une mesure importante en physique pour ce type d'objet. Merci d'avoir suivi la vidéo et à bientôt !

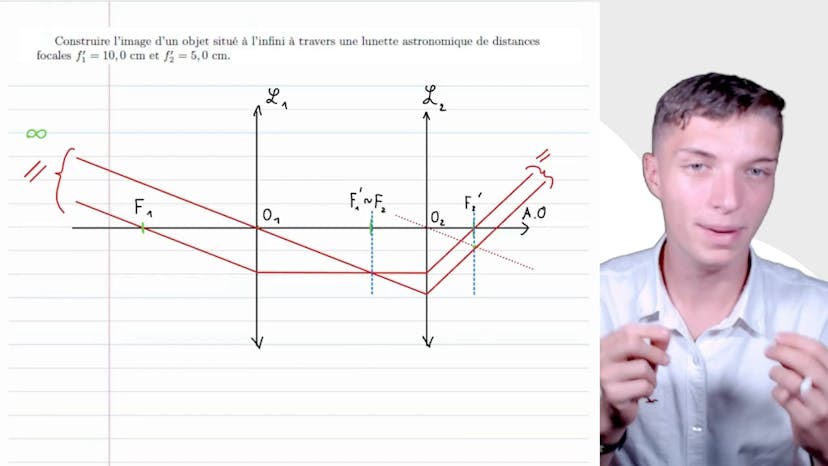
Schéma

Dans cette vidéo, Matisse de Studio explique le trajet d'un rayon lumineux à travers une lunette astronomique. La lunette est composée de deux lentilles convergentes, avec des distances focales f1' et f2'. Le foyer image de la première lentille est confondu avec le foyer objet de la deuxième lentille, ce qui rend le montage AFOC. Pour construire l'image d'un objet situé à l'infini, il faut tracer deux rayons. Le premier rayon passe par l'axe optique de la première lentille sans être dévié. Le deuxième rayon passe par le foyer image de la première lentille et est parallèle au premier rayon. Ensuite, le premier rayon entre dans la deuxième lentille parallèlement à l'axe optique, tandis que le deuxième rayon est tracé parallèlement à l'axe optique et passe par le centre de la deuxième lentille. L'intersection de ces deux droites donne la position de l'image de l'objet. Dans le cas d'une lunette astronomique, les rayons sortent de manière parallèle, ce qui donne l'impression de regarder l'infini. Il est important de refaire ce schéma plusieurs fois pour bien comprendre le tracé des rayons. Merci d'avoir suivi cette vidéo et à bientôt.

Zoom

Aucun résumé n'est disponible pour cette vidéo

Bonne configuration

Dans cette vidéo, on aborde la question de la configuration correcte d'une lunette astronomique. Trois schémas sont proposés, et il faut expliquer le choix. Pour cela, il faut comprendre ce qu'est un montage à focale, c'est-à-dire un système optique qui convertit un faisceau de lumière parallèle en un autre faisceau parallèle. Dans le cas d'une lunette astronomique, on sait que l'objectif reçoit d'abord les rayons, puis l'oculaire les reçoit ensuite, c'est-à-dire là où l'œil est placé. Pour différencier les deux premiers schémas, on peut considérer que si les rayons viennent de l'infini, ils doivent passer par f1' (le foyer image de l'objectif) avant de repartir vers l'infini, ce qui signifie qu'ils passent par f2 (le foyer objet de l'oculaire). Ainsi, pour un montage à focale, il est nécessaire que f1' et f2 soient confondus. Seul le premier schéma satisfait cette condition, donc c'est la bonne configuration pour une lunette astronomique à focale.

Montage afocal

Aucun résumé n'est disponible pour cette vidéo

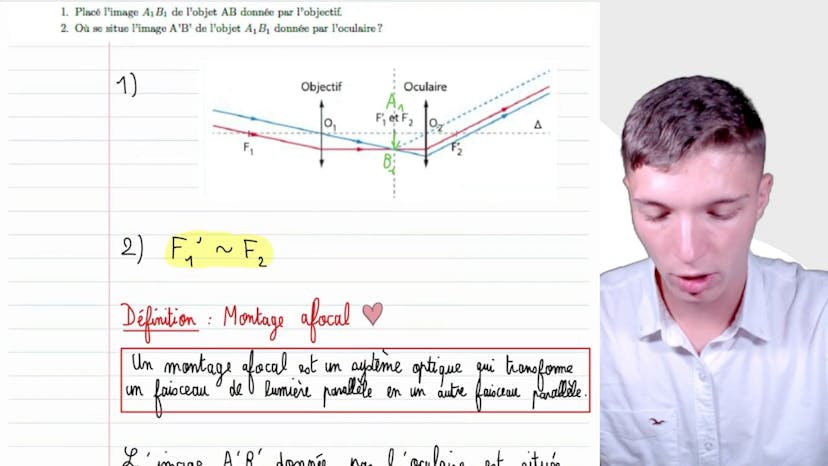
Image intermédiaire

Dans cette vidéo, Mathis explique comment placer une image intermédiaire à l'intérieur d'une lunette astronomique. Il commence par expliquer qu'il a tracé deux rayons issus d'un point B d'un objet AB situé à l'infini. Le point A est situé sur l'axe optique. Ensuite, il faut placer l'image A1, B1 de l'objet AB donné par l'objectif. Pour construire cette image, il faut se placer au niveau du point où les rayons se croisent, c'est-à-dire au niveau du foyer image de l'objectif ou du foyer objet de l'oculaire. A1 et B1 sont donc situés à cet endroit de croisement. L'image intermédiaire est donc bien placée dans la lunette astronomique. Ensuite, la vidéo aborde la question de l'emplacement de l'image A' B' de l'objet A1, B1 donné par l'oculaire. Mathis explique qu'il s'agit d'un montage infocal, ce qui signifie que F1' est confondu avec F2. Cela transforme un faisceau de lumière parallèle en un autre faisceau de lumière parallèle. Par conséquent, l'image A' B' donnée par l'oculaire est située à l'infini. C'est une notion cruciale à comprendre pour la lunette astronomique. À partir de cette image intermédiaire, puisqu'elle est placée au niveau du foyer objet de l'oculaire, elle ressortira à l'infini. En conclusion, Mathis remercie les spectateurs d'avoir suivi la vidéo et leur donne rendez-vous prochainement.

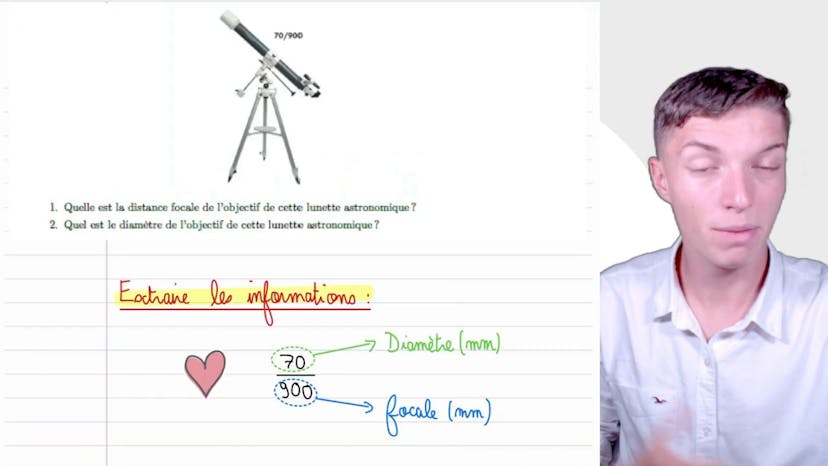
Dimensionnement

Dans cette vidéo, nous apprenons à dimensionner une lunette astronomique à partir de très peu d'informations. Sur la photo du télescope, nous pouvons voir les chiffres "70 sur 900". Pour déterminer la distance focale et le diamètre de l'objectif, nous devons extraire ces informations de ces chiffres. Le numérateur (70) correspond au diamètre de l'objectif, tandis que le dénominateur (900) correspond à la distance focale. Il est important de noter que ces chiffres doivent être adaptés aux unités appropriées, telles que les millimètres. Ainsi, pour cette lunette en particulier, le diamètre de l'objectif serait d'environ 70 millimètres et la distance focale serait d'environ 900 millimètres. Ces dimensions correspondent à celles attendues pour une lunette astronomique de cette taille. N'oubliez pas de retenir cette méthode pour extraire les informations à partir d'une seule grandeur afin de caractériser une lunette astronomique. Merci d'avoir regardé cette vidéo et à bientôt !

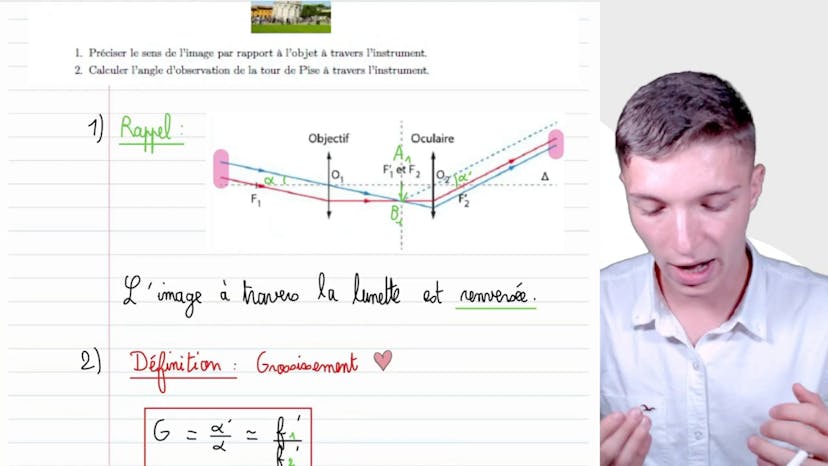
Tour de Pise

Dans cette vidéo, Matisse de Studio nous présente la Tour de Pise observée à travers une lunette astronomique. La distance de l'observation est de 57 mètres et le grossissement de la lunette est de 15. L'image observée à travers la lunette est renversée, ce qui est une caractéristique de ce type d'instrument. Pour calculer l'angle d'observation de la tour à travers la lunette, on utilise la définition du grossissement. Dans cet exemple, la tour a une taille apparente de 3,2 degrés, ce qui donne un angle d'observation de 48 degrés à travers la lunette. Ainsi, on peut observer la tour de Pise de manière beaucoup plus détaillée grâce à cette lunette astronomique. C'est la fin de cet exercice sur les caractéristiques de la lunette astronomique. N'hésitez pas à le revoir et à bientôt !

Anneaux de Saturne

Dans cette vidéo, nous abordons les travaux de Galilée sur les anneaux de Saturne. Le 25 juillet 1610, Galilée observe les anneaux de Saturne avec sa lunette astronomique. Nous cherchons à calculer l'angle d'observation alpha à l'œil nu en utilisant la tangente de cet angle. Nous obtenons un résultat de 7,2 x 10^-4 radian. Nous expliquons ensuite pourquoi les anneaux de Saturne n'ont pas pu être observés avant 1610 en raison de la sensibilité de l'œil humain et de la taille apparente des anneaux. Nous souhaitons ensuite observer l'image à travers la lunette avec un angle alpha prime de 0,10 radian, ce qui nécessite un grossissement de 139. En utilisant la définition du grossissement, nous exprimons le rapport entre les distances focales de l'objectif et de l'oculaire. Sachant que l'oculaire a une focale de 2 cm, nous calculons la distance focale de l'objectif, qui est de 2,78 m. Enfin, en utilisant la formule pour le dimensionnement d'une lunette astronomique, nous déduisons que la lunette doit mesurer au minimum 2,8 m. Voilà comment nous avons résumé ce cours sur les travaux de Galilée sur les anneaux de Saturne en termes SEO-friendly.

Double expression

Dans cette vidéo, Matisse de Studio nous explique le principe du grossissement en optique. Il commence par rappeler que dans une lunette astronomique, il y a un objectif de distance focale f1 prime et un oculaire de distance focale f2 prime. La première étape est de schématiser la situation, en représentant les différents angles du trajet du rayon lumineux. Ensuite, il montre comment, dans le cadre de petits angles, on peut démontrer que l'angle alpha est égal à a prime, b prime divisé par f1 prime, en utilisant la formule de la tangente. Il explique également que dans l'hypothèse des petits angles, la tangente de l'angle alpha est approximativement égale à l'angle lui-même. Il montre ensuite comment, dans le même principe, on peut montrer que l'angle alpha prime est égal à a prime, b prime divisé par f2 prime, en utilisant à nouveau la formule de la tangente. Enfin, il déduit le grossissement g, qui est égal à alpha prime sur alpha, en utilisant les résultats précédents. Il montre que le grossissement est égal à f1 prime divisé par f2 prime. En résumé, Matisse explique le principe du grossissement en optique, en montrant comment les angles alpha et alpha prime sont liés à la distance focale de l'objectif et de l'oculaire, et comment cela permet de calculer le grossissement.

Révisions Physique Lycée