 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Physique-Chimie
Physique
MPSI/PCSI

Glaçon
Aujourd'hui, nous étudions la fonte d'un glaçon dans un verre cylindrique contenant de l'eau liquide. Nous devons déterminer le volume immergé du glaçon en utilisant le principe d'Archimède et le principe fondamental de la dynamique. La poussée d'Archimède du glaçon est égale à son poids, donc nous pouvons calculer le volume immergé en utilisant les masses volumiques de l'eau liquide et de l'eau solide. Le volume immergé est donné par la formule : Vim = (ρgV0)/(ρ), où ρg est la masse volumique de l'eau liquide, V0 est le volume du glaçon et ρ est la masse volumique de l'eau solide. Ensuite, nous devons déterminer la différence entre la hauteur finale de l'eau (h1) après la fonte du glaçon et la hauteur initiale de l'eau (h0). En utilisant la conservation de la masse, nous pouvons établir que le volume du liquide une fois que le glaçon a fondu est égal au volume immergé. Finalement, nous examinons le cas où un glaçon d'eau pure est placé dans de l'eau salée. La masse volumique de l'eau salée est plus grande que celle de l'eau pure en raison de la présence de sel. En utilisant les mêmes principes, nous constatons que le volume immergé du glaçon est plus petit que le volume initial. Ainsi, lorsque le glaçon fond, la hauteur de l'eau dans le verre augmente. En résumé, nous utilisons les principes d'Archimède et le principe fondamental de la dynamique pour déterminer le volume immergé d'un glaçon et la différence de hauteur de l'eau avant et après sa fonte.
Physique-Chimie
Physique
MPSI/PCSI
Barrage
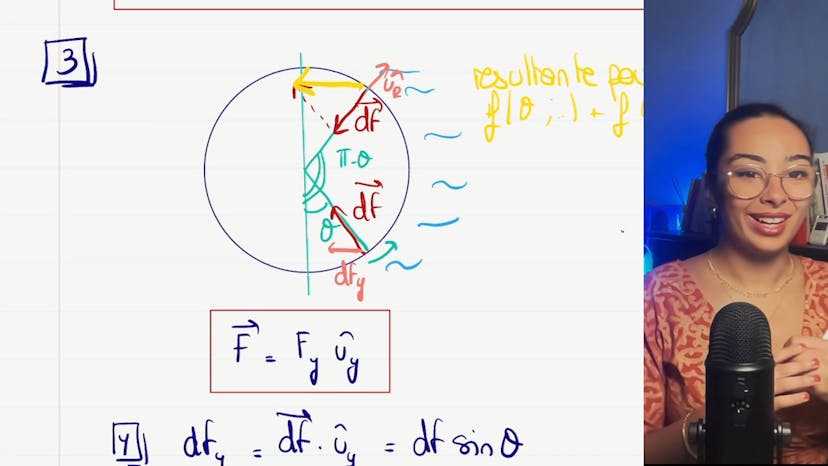
Dans cette vidéo, nous étudions la statique des fluides sur un barrage hémicylindrique. L'objectif est de calculer la résultante des forces de pression exercées sur le barrage.
Tout d'abord, nous déterminons la pression à l'altitude z en utilisant le principe fondamental de la statique. Nous trouvons que la pression p(z) est égale à p0 - ρgz - h, où p0 est la pression atmosphérique, ρ est la masse volumique de l'eau, g est l'accélération due à la pesanteur et h est la hauteur du barrage.
Ensuite, nous analysons la force élémentaire df exercée sur un élément de surface ds du barrage. Nous observons que cette force se compose de deux parties : la pression exercée par l'eau (p0) et la pression exercée par l'air (pr), qui agissent dans des directions opposées. Nous déterminons que la force élémentaire df est égale à -(ρgh - z) ds ur, où ur est un vecteur unitaire dans la direction radiale.
Pour obtenir la résultante des forces de pression, nous projetons les forces élémentaires sur la direction radiale (ur) et observons que les forces se compensent mutuellement, à l'exception de la composante verticale. Ainsi, la résultante des forces de pression est uniquement dans la direction verticale (uy). Nous trouvons que fy = -ρgh².
Finalement, nous commentons sur la conception du barrage et expliquons qu'il doit être solide et bien fixé au sol pour résister aux forces de pression de l'eau. Cela implique généralement l'utilisation de forces de frottement entre les fondations du barrage et le sol pour maintenir sa stabilité.
En résumé, nous avons étudié la statique des fluides sur un barrage hémicylindrique et calculé la résultante des forces de pression. Nous avons également discuté de l'importance de la conception et de la consolidation du barrage pour lui permettre de résister aux forces exercées par l'eau.
Physique-Chimie
Physique
MPSI/PCSI

Baromètre
Dans cet exercice de statique des fluides sur un baromètre, nous étudions la détermination de la hauteur d'un building situé à Taipei en utilisant la pression atmosphérique et l'intensité de la pesanteur. Nous utilisons le modèle de l'atmosphère isotherme pour déterminer l'expression de la masse volumique en fonction de la masse molaire de l'air.
Ensuite, nous utilisons cette expression pour obtenir une équation différentielle en P qui nous permet de déterminer la variation de pression en fonction de l'altitude. Nous déduisons ensuite le champ de pesanteur en fonction de l'altitude en utilisant la constante de gravitation universelle, le rayon de la Terre et un développement limité.
Nous étudions également la validité de l'hypothèse selon laquelle l'accélération de la pesanteur reste constante dans l'atmosphère. Nous calculons la différence relative de l'accélération de la pesanteur pour différentes altitudes et constatons qu'elle est insignifiante.
Ensuite, nous passons à l'étude du baromètre et déterminons la relation entre la pression atmosphérique et la hauteur mesurée avec le baromètre. Nous utilisons la loi de la statique des fluides pour relier la différence de pression entre deux points à la hauteur mesurée. Finalement, nous établissons le lien entre les millimètres de mercure et les pascals, une unité couramment utilisée pour exprimer la pression.
En résumé, cet exercice aborde la statique des fluides, l'utilisation du modèle de l'atmosphère isotherme, les développements limités, la vérification d'hypothèses et l'utilisation d'un baromètre pour mesurer la pression atmosphérique.
Physique-Chimie
Physique
MPSI/PCSI

Montgolfière
Le cours porte sur le décollage d'une montgolfière et l'application de la statique des fluides. Il explique que pour que la montgolfière puisse décoller, il faut trouver une condition sur la température minimale à l'intérieur de la montgolfière. Il aborde ensuite la masse volumique d'un gaz parfait et le modèle de l'atmosphère isotherme. Ensuite, le cours se concentre sur la montgolfière elle-même et demande de calculer la force ascensionnelle dans un format spécifique. Il aborde également la masse d'air emprisonnée et sa relation avec les forces de pression. La montgolfière décolle lorsque la force ascensionnelle est positive, ce qui impose une condition sur la température intérieure. Une température minimale de 377 Kelvin est calculée. Enfin, le cours demande de déterminer l'altitude maximale atteinte par la montgolfière, en utilisant la condition d'annulation de la force ascensionnelle. L'altitude maximale est calculée à 427 mètres. Le cours souligne l'importance de la cohérence des valeurs numériques et encourage à utiliser les outils et équations disponibles pour résoudre les questions.
Physique-Chimie
Chimie
MPSI/PCSI

Sens d'évolution
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Chimie
MPSI/PCSI

Avancement
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Chimie
MPSI/PCSI
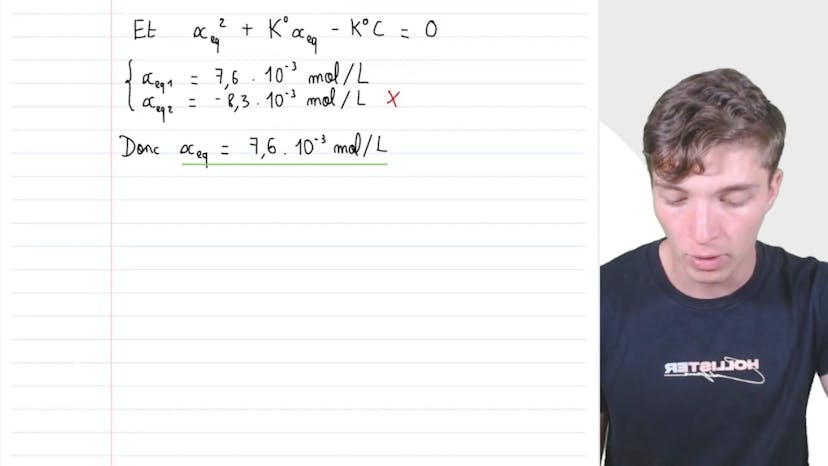
pH d'une solution
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Chimie
MPSI/PCSI

pH d'une solution (2)
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Chimie
MPSI/PCSI

pH d'un ampholyte
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Chimie
MPSI/PCSI

pH d'un mélange
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Chimie
MPSI/PCSI

Le Borax
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Chimie
MPSI/PCSI

L'acide acétique
Aucun résumé n'est disponible pour cette vidéo


