Cours d'apprentissage en ligne

Stats et Probas

Moyenne, écart-type, médiane

Dans cet exercice de statistique, nous utilisons la calculatrice pour déterminer différentes mesures pour une population de pitons. En utilisant les données fournies dans un tableau, nous insérons les tailles de pitons et leur nombre correspondant dans la calculatrice. Nous trouvons ensuite la moyenne de la population, l'écart-type, la médiane et l'écart interquartile en accédant au menu stats de la calculatrice. Les valeurs obtenues pour la moyenne, l'écart-type, la médiane et l'écart interquartile sont respectivement de 6,41, 1,05, 6 et 1.

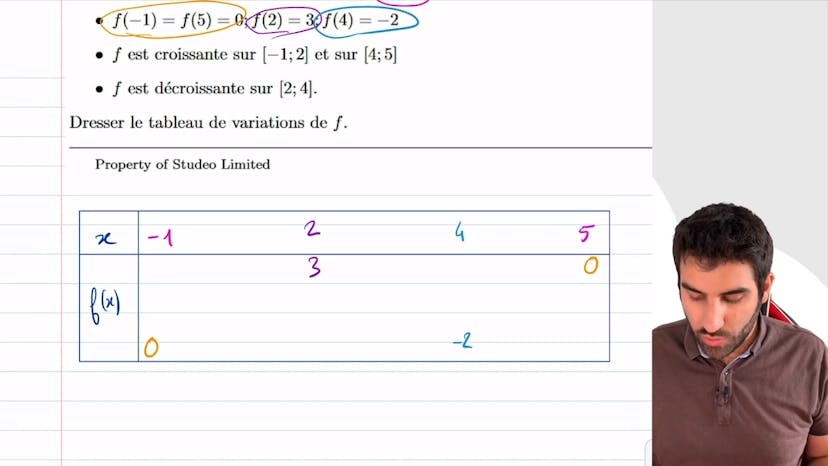
Tableau de variations 3 : tracé

Dans cet exercice, on apprend à dresser le tableau de variation d'une fonction en se basant sur plusieurs informations données. On commence par dessiner un tableau de variation standard qui a deux lignes et deux colonnes. La première ligne représente les valeurs de x, tandis que la deuxième ligne représente les valeurs de f (x) avec des flèches correspondantes aux variations. Ensuite, on remplit le tableau en utilisant les informations fournies. Si la fonction f est définie sur un intervalle donné, les bornes de cet intervalle seront les valeurs de x à gauche et à droite du tableau. On utilise ensuite les différentes informations pour remplir les cases du tableau. Les nombres sont mobiles et peuvent être déplacés en fonction des variations. Les flèches indiquent si la fonction est croissante ou décroissante sur l'intervalle donné. Une fois toutes les informations traitées, le tableau de variation de la fonction est complet.

Nombres et calculs

Résoudre une inéquation

Dans cet exercice, on apprend à résoudre une inéquation basique en isolant x. On doit notamment faire attention à changer le sens de l'inégalité quand on multiplie ou divise par un nombre négatif, et à appliquer les règles de la transformation d'un terme d'un côté à l'autre de l'inéquation. Ainsi, pour résoudre l'inéquation donnée, on procède à des calculs pour se débarrasser des termes en trop, en changeant le signe ou en divisant selon les cas. Finalement, on obtient la solution sous forme d'un intervalle. Dans ce cas, la solution est x supérieur ou égal à 1, ce qui correspond à l'intervalle fermé allant de 1 à l'infini.

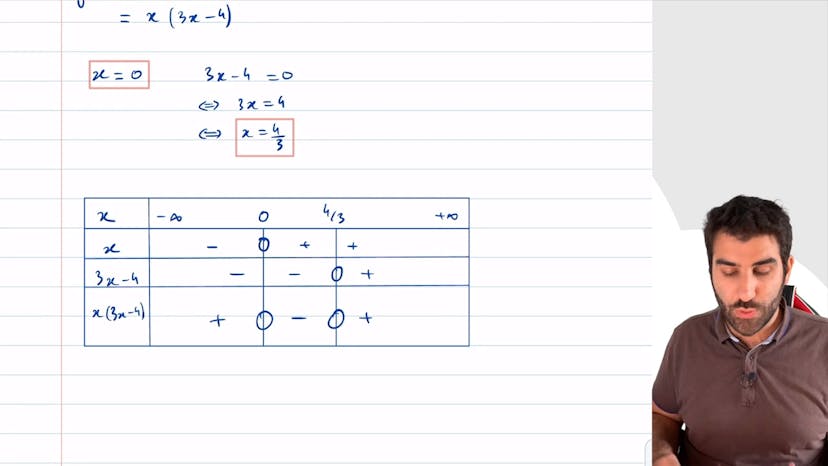
Factorisation et tableau de signes

Cet exercice consiste à dresser le tableau de signe d'une fonction à partir de son expression factorisée. Il est important de factoriser avant de faire le tableau de signe. On cherche ensuite les valeurs pour lesquelles chaque facteur s'annule (x=0 et x=4/3 dans cet exemple), puis on remplit les signes en se rappelant la règle de signes pour les expressions affines et en utilisant la règle de signes pour le produit final.

Antécédent et Image

Dans cette leçon, nous apprenons comment savoir si un point appartient à la courbe d'une fonction en utilisant ses coordonnées. Si un point M a des coordonnées xm, ym et appartient à la courbe d'une fonction, alors l'ordonnée de M est égale à f de son abscisse. Nous pouvons également dire que chaque point sur la courbe d'une fonction vérifie que son ordonnée est égale à f de son abscisse. Pour vérifier si un point appartient à la courbe d'une fonction, nous devons simplement calculer f de son abscisse et voir si cela correspond à son ordonnée. Si oui, le point appartient à la courbe de la fonction. Sinon, il n'y appartient pas. Dans notre exemple, nous avons calculé g de moins 2 pour trouver que l'abscisse de a est bien égal à son ordonnée, donc le point a appartient à la courbe de g.

Tableau de variations 2 : comparaison

Dans cet exercice de mathématiques, on apprend à utiliser le tableau de variation d'une fonction pour comparer deux images de cette fonction. Les images de la fonction sont placées sur le tableau en fonction de leurs antécédents. En utilisant ces informations, on peut déterminer que f de "-4" est entre "-13" et "-6", et que f de 6 est entre 2 et 8. Grâce à la transitivité d'inéquation, on peut conclure que f de "-4" est plus petit que f de 6.

Géométrie

Equation cartésienne

Dans cet exercice, nous allons apprendre comment déterminer si un point donné appartient à une droite dont l'équation est connue. La méthode est la même pour l'équation cartésienne ou réduite de la droite. Pour cela, nous remplaçons les coordonnées du point dans l'équation de la droite et si l'égalité est vérifiée, le point appartient à la droite. Dans le cas contraire, le point n'appartient pas à la droite. Par exemple, en remplaçant les coordonnées du point c dans l'équation de la droite, nous avons obtenu un résultat différent de zéro, ce qui signifie que le point c n'appartient pas à la droite.

Reconnaître des fonctions

Dans cet exercice, nous traduisons des informations sur des fonctions en écriture explicite. La première fonction est affine avec une écriture de 3x-2. La deuxième fonction affine est de 2x-2 plus 6. La troisième fonction est une fonction carrée avec une écriture de x². La quatrième fonction est une fonction inverse avec une écriture de 1 sur x. Connaissant le fait que les fonctions affines passent par zéro et la fonction carrée s'annule également en zéro, la fonction inverse n'a pas d'antécédent par cas et n'est pas définie en zéro. La fonction carrée est la seule fonction restante qui peut avoir plusieurs antécédents. La fonction g est croissante sur son ensemble de définitions, ce qui signifie que la fonction g est 3x-2 et la fonction h est -2x plus 6.

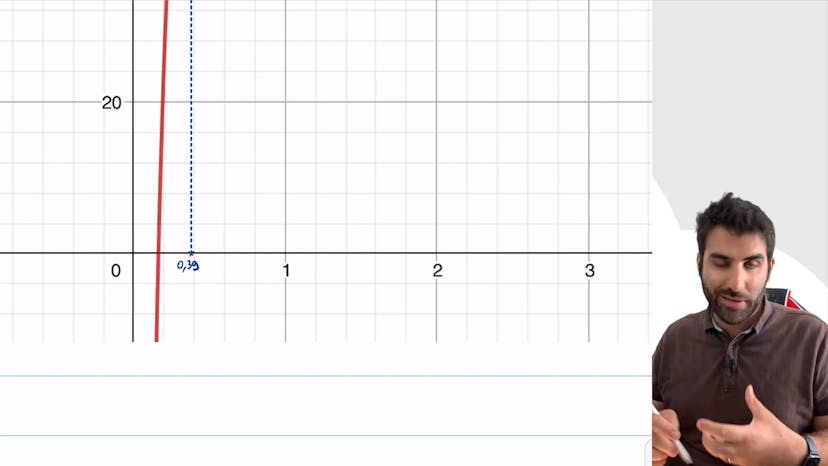
Résolution graphique : équation

L'exercice consiste à trouver graphiquement l'égalité entre f(x) et g(x) en tracant les courbes. Le point d'intersection des deux courbes est important car il donne l'abscisse du ou des points d'intersection, selon s'il y en a plusieurs. Pour résoudre graphiquement f(x) = g(x), il suffit de lire l'abscisse des points d'intersection. Dans cet exercice, le point d'intersection a une abscisse d'environ 0,39, il est donc possible de dire que f2x égale g2x a pour solution x est égal à 0,39. Il est important de noter que la précision n'est pas nécessaire, une approximation suffit.

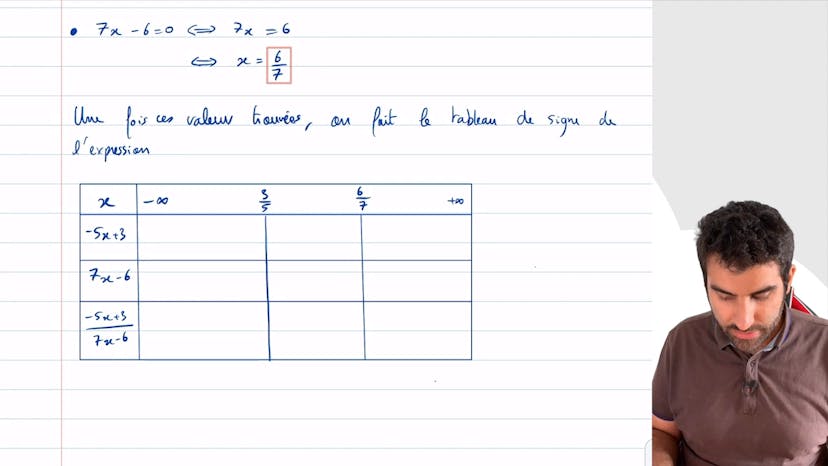
Tableau de signes pour un quotient

Dans cet exercice, il est expliqué comment déterminer le signe d'une fonction. Pour ce faire, il faut d'abord résoudre les équations pour trouver les valeurs de x pour lesquelles le numérateur et le dénominateur s'annulent. Puis, on crée un tableau de signes en mettant sur chaque ligne les valeurs de x pertinentes, les facteurs de l'expression et le bilan du produit ou quotient. Les bornes de l'ensemble de définition sont également indiquées. Les zéros sont placés à l'endroit où chaque ligne s'annule. Les lignes affiliées à une expression affine, c'est-à-dire celle ax+b, prennent le signe positif avant zéro et le signe négatif après. Une double barre est utilisée pour les valeurs interdites. Ensuite, on utilise la règle des signes pour remplir la dernière ligne du tableau. À partir de ce tableau, on peut déduire le signe de la fonction.

Stats et Probas

Arbre de probabilités

Dans cet exercice, on cherche à savoir la probabilité d'obtenir exactement une boule blanche à l'issue de deux lancers. Pour y parvenir, on modélise la situation avec un arbre de probabilité en prenant en compte la remise des boules après chaque tirage. En examinant les différents cheminements possibles, seuls deux cas de figure nous intéressent : boule noire puis boule blanche et boule blanche puis boule noire. La probabilité de chacun de ces deux cas de figure est de 6 sur 25 et on obtient une probabilité de 12 sur 25 en additionnant les deux. Ainsi, la probabilité de tirer exactement une boule blanche est de 12 sur 25.

Nombres et calculs