Cours d'apprentissage en ligne

Mouvement sur une ellipse

Dans ce cours, on apprend à calculer le mouvement d'un point M qui se déplace sur une ellipse. On utilise l'équation cartésienne de l'ellipse pour déterminer les coordonnées du point M à différents moments. On montre également comment déduire la valeur de bêta en utilisant l'équation de l'ellipse. On calcule ensuite la vitesse et l'accélération du point en dérivant les équations horaires de M. Finalement, on montre que l'accélération a est de la forme -oméga carré om, qui correspond à un mouvement d'oscillateur harmonique. On souligne l'importance de connaître les ellipses en physique et en mécanique, car elles apparaissent souvent dans l'étude des mouvements planétaires.

Pendule

Le cours parle du pendule simple en physique, où un point est attaché à un fil de longueur L fixé à un point O. Le mouvement est enregistré en coordonnées polaires, et on observe des oscillations pendulaires. Les vecteurs position, vitesse et accélération sont ensuite déterminés en utilisant des coordonnées polaires et cartésiennes, en changeant l'origine du repère. Il est important de connaître les dérivées des vecteurs de base pour résoudre les problèmes et manipuler les différents repères. Les oscillateurs harmoniques sont souvent observés dans les mouvements décrits.

Chute libre

Dans ce cours, Leïla explique comment calculer l'équation de la trajectoire pour une chute libre sans frottement. Elle rappelle que la caractéristique principale de la chute libre est l'absence de force autre que la pesanteur. Elle utilise des équations mathématiques pour exprimer la vitesse et la position de l'objet en fonction du temps, puis elle isole le temps pour obtenir l'équation de la trajectoire en fonction de la position. Elle souligne que la maîtrise de ces équations est importante pour résoudre des problèmes plus complexes liés à la chute libre. Elle invite les spectateurs à poser des questions en commentaire.

Pendule simple

La vidéo traite de l'équation différentielle vérifiée par un pendule simple. La personne commence par faire un bilan des forces en coordonnées polaires, avec le poids et la tension du fil. Elle utilise ensuite le principe fondamental de la dynamique pour obtenir l'équation du mouvement pour le pendule simple en coordonnées polaires. Elle montre également comment obtenir l'oscillateur harmonique de pulsation propre à sin2g sur L dans la limite des petits angles. L'ensemble des équations sont présentées avec des explications sur les signes à vérifier en coordonnées polaires.

Livre sur une table

Cet exercice de dynamique du point consiste à déterminer la réaction normale exercée par une table sur un livre et un verre posés dessus. On fait un bilan des forces pour le système livre plus verre dans son ensemble en prenant en compte la réaction de la table et le poids total, et on trouve l'expression de la réaction normale. Ensuite, on regarde le système constitué uniquement du livre en prenant en compte la réaction de la table et la force exercée par le verre sur le livre, qu'on détermine en regardant le système constitué uniquement du verre. En utilisant le principe d'action-réaction, on obtient la même expression pour la réaction normale. Il faut faire attention aux systèmes d'études choisis et aux forces extérieures.

Chute libre 2

Cet exercice porte sur la chute libre d'un objet lancé depuis l'origine d'un repère cartésien avec une vitesse initiale formant un angle alpha avec l'horizontale. On cherche à déterminer les grandeurs cinématiques et l'instant où le point passe par une altitude maximale dans le cas avec et sans frottement. Sans frottement, l'objet est soumis seulement à son poids, ce qui permet de déterminer facilement les grandeurs cinématiques. Avec frottement, il faut prendre en compte une force de frottement fluide, ce qui conduit à une équation différentielle pour les trajectoires en x et y. Pour déterminer l'instant où l'altitude est maximale, on cherche à annuler la vitesse verticale. Dans le cas sans frottement, on trouve facilement l'instant, tandis que dans le cas avec frottement, il faut résoudre une équation plus compliquée en isolant le temps. Il est important de faire le lien entre les deux modélisations et de vérifier que l'on retrouve la même expression pour des très petits frottements.

Système masse-ressort

Dans ce cours, nous étudions un système masse-ressort horizontal. Nous examinons l'équation d'un tel système, en faisant un bilan des forces appliquées sur une masse accrochée à un ressort horizontal avec une constante de raideur k et une longueur à vide L0 qui se déplace selon ux. Nous établissons l'équation du mouvement et expliquons comment la simplifier en utilisant un changement de variable pour l'écart à la position d'équilibre. Nous arrivons à une équation différentielle d'un oscillateur harmonique à la pulsation racine de k sur m, oméga 0. Il est important de savoir résoudre cette équation différentielle pour réussir certains concours.

Saut sur la Lune

Dans ce cours, Leïla explique un exercice sur le saut sur la lune, qui est une variante de la chute libre. Le but est de passer du champ de pesanteur terrestre au champ de pesanteur lunaire en étudiant le système et le référentiel dans lequel on étudie le mouvement. Elle propose de faire un bilan des forces et de réaliser un schéma à l'instant quelconque pour y faire figurer les différentes forces. On doit établir les équations horaires du mouvement à accélération constante et passer à la trajectoire en éliminant le temps au profit de x. Lorsqu'il touche le sol, c'est quand z de xf où x c'est la pièce où on touche le sol est nulle. On peut ensuite calculer la distance de saut horizontale sur la lune de 9 mètres en modifiant l'accélération de la pesanteur de la Terre.

Iceberg

Cet exercice consiste à déterminer la proportion de glace immergée dans un iceberg à partir d'une photo en utilisant les compétences de mécanique vues dans ce chapitre. On donne la masse volumique de la glace ρg et celle de l'eau ρm. La force de pesanteur est égale à –mgEz vers le bas et la poussée d'Archimède correspond au poids du fluide déplacé vers le haut, exprimée parfois par PiA ou PA. L'équilibre mécanique de l'iceberg permet de trouver la proportion volumique de glace immergée qui est égale à 90%.

Chaussette dans un sèche-linge

Le cours porte sur la modélisation du mouvement d'une chaussette dans un sèche-linge en deux phases: une phase de rotation circulaire et une phase de chute libre. Le rayon du cylindre du sèche-linge est de 25 cm, tournant à 50 tours par minute, et la chaussette est assimilée à un point matériel de masse m. L'accélération est calculée dans une base polaire et la réaction du tambour sur la chaussette est déduite en utilisant le principe fondamental de la dynamique. Le décollement se produit lorsque la réaction normale s'annule, conduisant à un mouvement de chute libre. Le mouvement ultérieur est décrit comme étant parabolique. Le mouvement est cyclique car le décollement se produit toujours au même endroit.

Glissade sur un igloo

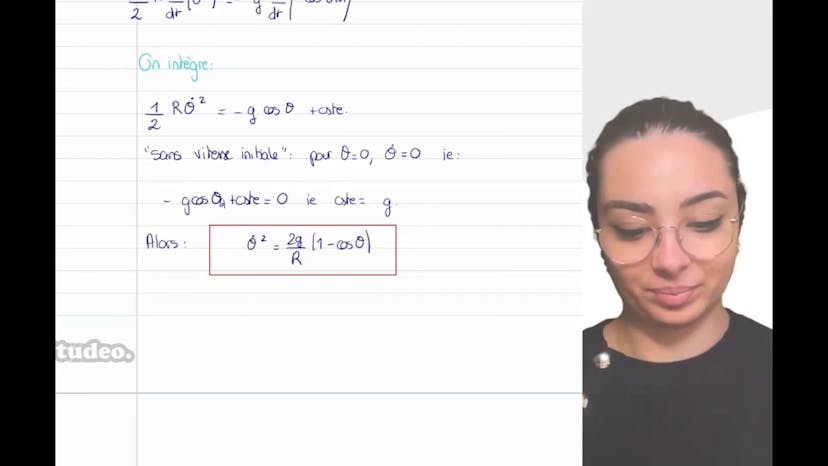
Dans cet exercice de dynamique, on étudie le mouvement d'un enfant esquimau qui glisse sur un igloo sphérique de rayon R. Pour déduire les équations de mouvement, on applique le théorème de la résultante cinétique à l'enfant, qui est soumis à son poids et à la réaction normale du support du igloo, mais sans frottement. On obtient ainsi deux équations différentielles portant sur l'angle θ, dont l'une permet de déterminer la réaction normale. En multipliant la première équation par θ, on montre une identité qui porte sur θ², ce qui permet de déterminer l'expression de cette dernière en fonction de θ. En injectant cette expression dans la deuxième équation, on déduit l'expression de la force de réaction du igloo. Enfin, en utilisant la condition de décollement (Rn = 0), on trouve que l'enfant décolle du igloo avant d'atteindre le sol pour un angle θ inférieur à π/3.