All subjects
All subjects
 All subjects
All subjects
Fonction Composée
Dans ce cours, nous étudions une fonction composée et comment faire l'étude et le tableau de variation d'une fonction qui est composée de deux autres fonctions.
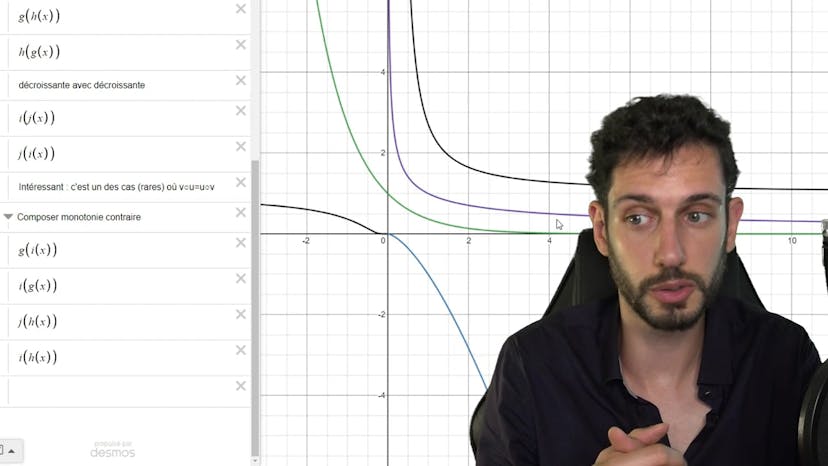
Dans cet exemple, la fonction proposée est E2-1 sur x². Nous identifions les fonctions composantes de la fonction, g et h. La fonction g est -1 sur x², définie et dérivable sur R, tandis que la fonction h est l'exponentielle, définie et dérivable sur R.
Nous utilisons les formules de dérivation pour trouver la dérivée de g, qui est 2 sur x³. Nous déterminons les variations de g en utilisant le signe de sa dérivée. Ainsi, on obtient un tableau de variation de g, qui est décroissante de moins l'infini à 0 et croissante de 0 à plus l'infini.
Nous calculons également les limites de la fonction g, qui sont 0 en moins l'infini et moins l'infini en 0+.
Ensuite, nous analysons la fonction h, qui est croissante sur R. En combinant les sens de variation de g et h, nous pouvons déduire les variations de la fonction composée, F. F sera donc décroissante sur R étoile moins et croissante sur R étoile plus.
Nous calculons également les limites de F en utilisant les limites des fonctions composantes. La limite de F en moins l'infini est 1 et en plus l'infini est également 1. En 0, la limite de F est 0.
Enfin, nous construisons le tableau de variation de F, qui est décroissante de 1 à 0 et croissante de 0 à 1.
La fonction n'est pas définie en 0, mais peut être prolongée par continuité en posant F de 0 égale à 0.
Une autre méthode aurait été de calculer directement la dérivée de F, mais nous avons choisi ici d'étudier l'intérieur de la composition.
Si vous avez des questions, n'hésitez pas à les poser sur la FAQ.