Master Fundamental Concepts in Math, Physics, and Chemistry - with Courses and Video Solutions by Specialist Teachers.

Physiques Chimie

Révisions Maths lycée

Probas Terminale

Principe multiplicatif

Dans cet exercice sur les échanges de poignées de mains entre deux équipes de 15 personnes, on cherche à déterminer le nombre de poignées de mains échangées. Pour résoudre ce problème, il faut analyser la notion de poignée de main en tant que lien entre deux personnes appartenant à des équipes différentes. On peut donc former une paire en choisissant une personne de l'équipe 1 et une personne de l'équipe 2. Il y a 15 possibilités dans l'équipe 1 et 12 possibilités dans l'équipe 2, ce qui donne un total de 180 poignées de mains possibles. Il est important de noter que chaque poignée de main est comptée une seule fois, car on a établi une liste où le premier élément vient de l'équipe 1 et le second élément vient de l'équipe 2. Ainsi, on évite de compter deux fois la même paire en inversant les rôles des équipes. En comprenant qu'il s'agit de compter des paires, le problème devient plus simple à résoudre.

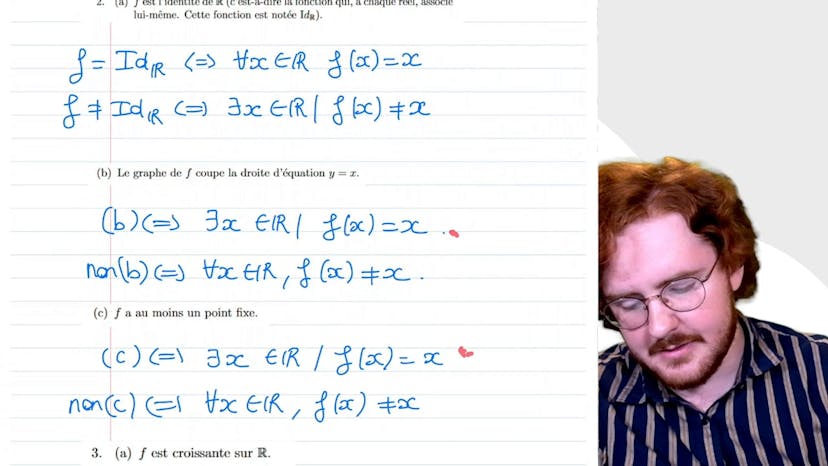
Utiliser les quantificateurs

Dans cette vidéo, Paul explique comment traduire des phrases logiques en français en utilisant des quantificateurs mathématiques. Il utilise des exemples avec une fonction f de r à R et explique comment exprimer ces phrases à l'aide de quantificateurs et leur négation. Les exemples incluent des questions sur l'unicité de solutions, l'existence de points fixes, la croissance/decrémentation de la fonction et l'annulation de la fonction sur R. Paul souligne qu'il y a différentes façons de décrire la même chose avec des quantificateurs et il explique comment prendre la négation d'une implication en utilisant la logique "a et non b". En somme, cette vidéo est un guide pour comprendre et utiliser correctement les quantificateurs mathématiques pour traduire des phrases logiques en français.

Ecrire la négation

Dans cette vidéo, on apprend comment traduire des assertions en français en des assertions logiques avec des quantificateurs, cet exercice se concentre sur des suites réelles UN définies sur N. Pour exprimer que l'assertion "la suite UN est majorée", il faut dire qu'il existe un nombre M appartenant à R tel que, pour tout N appartenant à N, UN est inférieur ou égal à M. En négatif, il faut dire que, quel que soit M appartenant à R, il y a au moins un rang N tel que UN est supérieur à M. Pour l'assertion "la suite UN est bornée", elle est équivalente à dire qu'il existe un petit M et un grand M appartenant à R² tels que, pour tout N appartenant à N, UN est compris entre petit M et grand M. En négatif, il faut dire soit qu'elle est non bornée car il existe un rang N tel que UN est strictement inférieur à petit M pour tout M appartenant à R, soit qu'elle est non bornée car il existe un rang N à partir duquel UN est strictement supérieur ou égal à tout M appartenant à R. Pour l'assertion "la suite UN est décroissante", il suffit de dire que, pour tout N appartenant à N, UN est inférieur à UN plus 1. En négatif, il faut dire qu'il existe un rang N tel que UN est supérieur à UN plus 1. Enfin, pour l'assertion "la suite UN est monotone", elle est soit croissante, soit décroissante, il faut donc utiliser le quantificateur "quel que soit" avec chaque affirmation.

Equivalence et implication

Dans ce cours, Paul explique comment utiliser les implications et les équivalences en résolvant des problèmes logiques. Il donne trois exemples de problèmes et explique comment déterminer si l'équivalence ou l'implication est réciproque ou directe. Le premier problème concerne x appartenant à R tel que x² égale à 4, Paul parvient à prouver que l'implication est seulement dans le sens retour. Le deuxième problème concerne z qui est un complexe et si z est égal à son conjugué, est-ce que z appartient à R ? Paul parvient à prouver que l'équivalence est vraie. Le troisième problème concerne x appartenant à R tel que x égale à pi et e2i x égale à 1. Paul parvient à prouver que l'implication est seulement dans le sens direct.

Raisonner par l'absurde

Dans cette vidéo, Paul démontre que si a et b sont deux entiers tels que a plus b racine de 2 égal à 0, alors a = b = 0. Il utilise la logique par l'absurde en supposant que a ou b est différent de 0 et montre que cela mène à une contradiction. Ensuite, il démontre que si m plus n racine de 2 égal à p plus q racine de 2 pour des entiers m, n, p et q, alors m = p et n = q. Il utilise le résultat de la première partie et arrive à cette conclusion en rassemblant les termes et en montrant que n moins p et n moins q sont égaux à 0. Cette vidéo est utile pour comprendre la logique impliquée dans les preuves mathématiques.

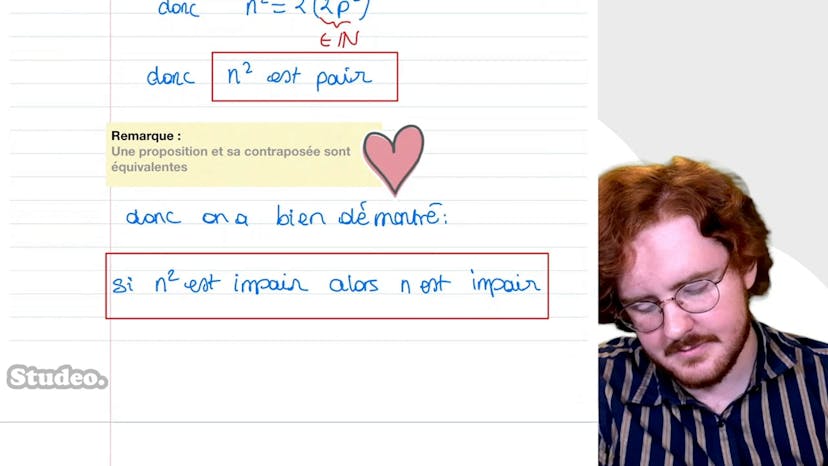
Raisonner par contraposée

Dans ce cours sur la démonstration par la contraposée, Paul explique comment démontrer une proposition en utilisant sa contraposée qui consiste à inverser la relation et les termes. Pour illustrer cela, il prend l'exemple de la proposition suivante: si n² est impair, alors n est impair. En utilisant la contraposée, il dit que si n est pair, alors n² est pair. Ensuite, il démontre cette contraposée en expliquant qu'un nombre pair peut être représenté comme 2p et donc n² sera égal à 2 facteurs de 2p², ce qui est pair. Il conclut en expliquant que quand la contraposée est plus facile à démontrer, on peut l'utiliser pour démontrer la proposition initiale.

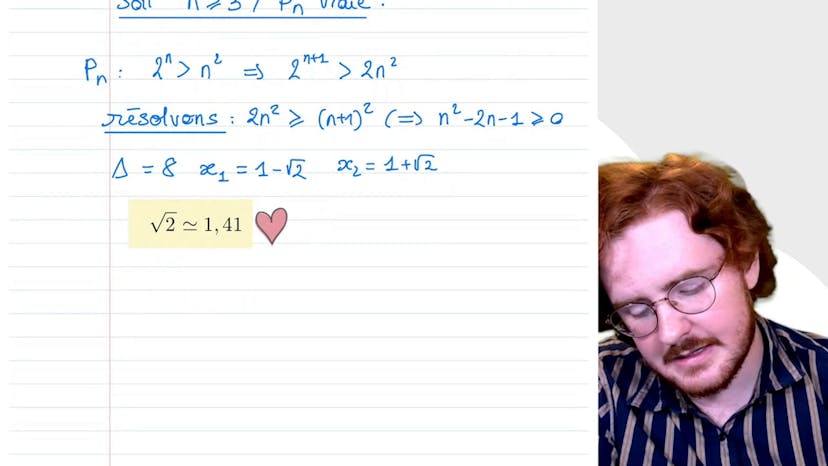
Raisonner par récurrence

Paul explique comment travailler le raisonnement par récurrence en démontrant la propriété pn ≥ n² pour n appartenant à n. Pour prouver la récurrence, il utilise une implication qui montre que si pn est vraie, alors pn plus 1 est également vraie pour n supérieur ou égal à 3. Il démontre ensuite l'initialisation pour n égal à 3, qui se révèle fausse en testant la propriété. En testant les valeurs supérieures de n, il trouve que pour n égal à 5, la propriété est vraie. Ainsi, il conclut que la propriété est vraie pour tout n supérieur égal à 3, et que le rang cherché est 5.

La récurrence forte

Dans ce cours, Paul explique comment utiliser le raisonnement par récurrence pour démontrer une relation de récurrence forte. Il donne l'exemple d'une suite u1 définie par u1 = 3 et la somme des n premiers termes de la suite divisée par deux fois n pour toute n. On veut démontrer que pour toute n, u1 est égale à 3n. Paul définit une propriété pn (récurrence forte) pour montrer que tous les uk sont égaux à 3k et pas seulement u1 = 3n. Il effectue ensuite une initialisation (n = 1) et démontre l'hérédité pour n + 1 en deux cas: k appartient à 1 à n et k = n + 1. Lorsque k appartient à 1 à n, la propriété est prouvée car on sait que tous les uk sont égaux à 3k grâce à pn. Ensuite, en remplacant les ui par 3j, on obtient la somme des j allant de 0 à n, qui est égale à n(n+1)/2. Après avoir simplifié, on obtient 3n, ce qui prouve que pn + 1 est vrai. Ainsi, pn est vrai pour tout n et un est égal à 3n pour tout n.

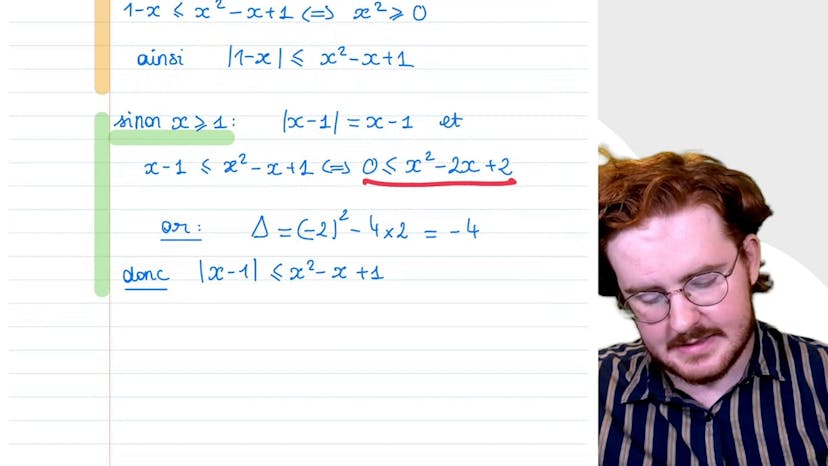
La disjonction de cas

Dans cette vidéo, Paul explique le raisonnement par disjonction de cas avec pour exemple une équation à démontrer. Il montre comment enlever la valeur absolue de la variable x en divisant les cas en deux parties: si x est inférieur à 1 ou si x est supérieur ou égal à 1. Dans le premier cas, il développe la formule pour montrer que l'inégalité est vraie, et dans le deuxième cas, il montre que le polynôme est toujours positif, ce qui prouve également que l'inégalité est vraie. Finalement, il démontre que pour tout x réel, la valeur absolue de x-1 est inférieure ou égale à x²-x plus 1.

Analyse-Synthèse

Dans cette vidéo, Paul explique comment résoudre un exercice en utilisant un raisonnement d'analyse synthèse en SEO friendly. L'exercice consiste à déterminer les réels x tels que racine de 2-x est égale à x. Pour commencer, on fait une analyse en supposant qu'il existe un x tel que l'énoncé soit vrai. On trouve que x doit être supérieur à 0 et qu'il est égal à 1 si on résout le polynôme obtenu. Cela prouve l'unicité de x, mais pas son existence. Pour prouver son existence, on vérifie si la relation fonctionne pour x=1, ce qui est le cas. Ainsi, on trouve que x est égal à 1 et est l'unique réelle vérifiant la condition.

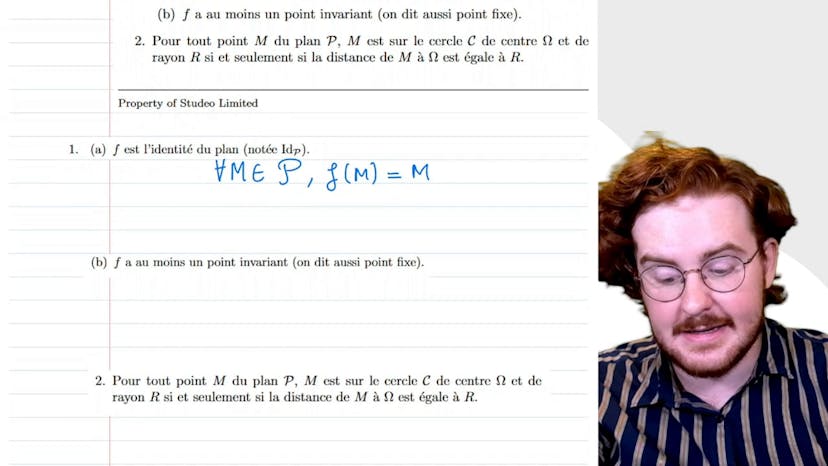
Quantificateurs un peu chauds

Dans cette vidéo, Paul explique l'importance des quantificateurs en mathématiques en utilisant l'exemple d'une fonction f du plan dans lui-même. Il explique que le plan P est un ensemble au même titre que R et que cela ne change rien quant aux quantificateurs utilisés. Il traduit ensuite l'affirmation que f est l'identité du plan en utilisant des quantificateurs, et explique comment on peut également traduire la négation de cette affirmation. Enfin, il explique comment traduire l'affirmation que pour tout point M du plan P, M est sur un cercle C de centre oméga et de rayon R si et seulement si la distance de M à oméga est égale à R, en utilisant des quantificateurs.