Home

MPSI/PCSI

Maths

Analyse

Logique

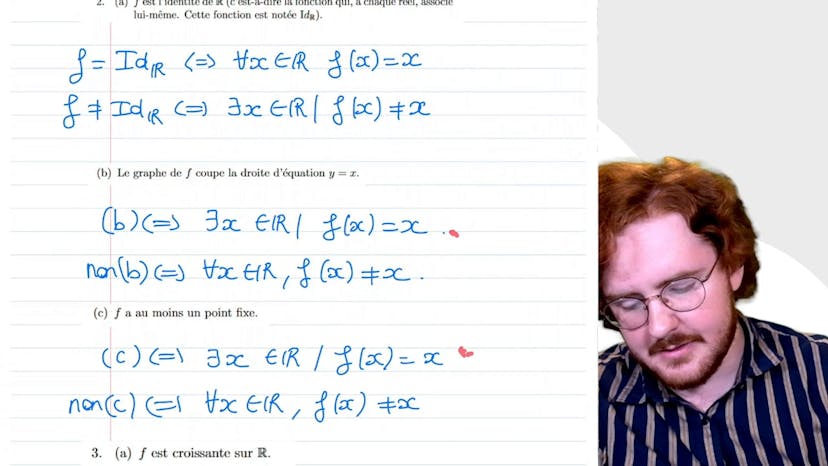
Dans cette vidéo, Paul explique le raisonnement par disjonction de cas avec pour exemple une équation à démontrer. Il montre comment enlever la valeur absolue de la variable x en divisant les cas en deux parties: si x est inférieur à 1 ou si x est supérieur ou égal à 1. Dans le premier cas, il développe la formule pour montrer que l'inégalité est vraie, et dans le deuxième cas, il montre que le polynôme est toujours positif, ce qui prouve également que l'inégalité est vraie. Finalement, il démontre que pour tout x réel, la valeur absolue de x-1 est inférieure ou égale à x²-x plus 1.

Salut c'est Paul et on se retourne dans une nouvelle vidéo où on va voir un cas de raisonnement par disjonction de cas. Ok, donc qu'est ce que c'est qu'une disjonction de cas? On va le voir avec cet exemple. Donc on va démontrer que pour toute x appartenant à R, la valeur absolue de x-1 est inférieure ou égale à x²-x plus 1. Ok, donc soyez que ça appartenant à R et là on va faire une disjonction de cas parce qu'en fait cette inéquation là elle est facile à résoudre dans si il n'y avait pas sa valeur absolue. Ses valeurs absolues en fait on peut les enlever en divisant deux cas. Si x est strictement inférieur à 1, et bien donc ça va être notre premier cas, et bien la valeur absolue de x-1 est égale à 1-x. Et ce qu'on veut démontrer ici, c'est équivalent à x² est supérieur à 0 si on remet tout du bon côté. Donc ça c'est toujours vrai, ainsi on a bien l'inégalité qu'on veut. Ainsi on a l'inégalité qu'on veut. Donc après on a le deuxième cas, si x est supérieur ou égal à 1, donc là on a bien couvert tous les cas, soit x est strictement inférieur à 1, soit x est supérieur ou égal à 1. Donc la valeur absolue de x-1 est égale à x-1, et on peut réécrire notre inéquation qui est équivalente à 0 et donc qui est équivalente à x²-2x plus 2 est supérieur ou égal à 0. Donc là on a un polynôme, on calcule son déterminant qui est égal à moins 4, donc il n'y a pas de solution. Or on voit que ce polynôme pointe vers le haut, donc ça veut dire que ce polynôme est toujours positif. Donc ça c'est bien vrai, donc on a l'inégalité qui est bien vraie, ainsi on a prouvé notre inégalité dans le deuxième cas. Donc, quel que soit x appartenant à R, la valeur absolue de x-1 est inférieure à x²-x plus 1. Voilà, on se dit à la prochaine fois!

La disjonction de cas

RELATED

Recommended videos

Utiliser les quantificateurs

Ecrire la négation

Equivalence et implication