Home

Révisions Maths lycée

Analyse Terminale

Déf&Propriétés

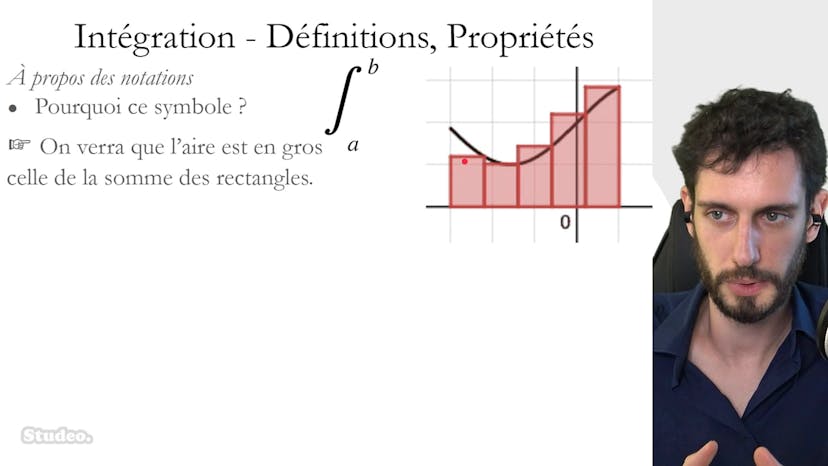
L'intégrale d'une fonction continue et positive sur un intervalle [a, b] représente l'aire sous la courbe de cette fonction entre les valeurs de x égales à a et b, ainsi que l'axe horizontal. On peut également l'appeler "aire sous la courbe de f sur l'intervalle [a, b]". L'unité d'aire utilisée peut varier en mathématiques, mais on utilise généralement un carré de taille 1 sur 1 comme unité d'aire. L'intégrale est notée "∫f(x) dx", c'est-à-dire le symbole mystérieux que l'on découvre en mathématiques. 

Si la fonction f(x) est négative sur l'intervalle [a, b], l'intégrale sera calculée comme la surface S mesurée sous la courbe, mais avec un signe négatif. En d'autres termes, on considère que c'est une surface négative. Dans le cas où la fonction f(x) présente des parties positives et des parties négatives sur l'intervalle, l'intégrale sera la somme des aires sous les parties positives et la soustraction des aires sous les parties négatives. Il est important de noter que l'intégrale est positive quand la fonction est au-dessus de l'axe horizontal, et négative quand elle est en dessous. N'hésitez pas à poser des questions supplémentaires.

Définition d'une intégrale. Pour f, une fonction continue et positive sur un intervalle a, b permet. On appelle intégrale de a à b de la fonction f, l'aire de la surface qui est délimitée par la fonction f elle-même et par les axes verticaux x égale a, x égale b, ainsi que l'axe horizontal o, x. En gros, c'est l'aire sous la courbe. Si on le dit en mots tranquilles, on appelle ça domaine sous la courbe de f sur l'intervalle a, b, mais on peut appeler ça r sous la courbe. On l'exprime en unité d'air. L'unité d'air, c'est, si vous voulez, quand vous avez un repère orthonormé, vous pouvez dire que le petit carré de taille 1 entre 0i et 0j est une unité d'air. Ce n'est pas toujours des centimètres carrés, donc on appelle ça génériquement en maths, pour ne pas vous mettre de centimètres ou de millimètres. C'est juste un petit carré de taille 1 sur 1, c'est une unité d'air. On la note. Intégrale, c'est une espèce de signe mystérieux qu'on découvre en maths. Intégrale entre a et b de f de x, dx. On va voir un peu dans plusieurs vidéos pourquoi cette écriture, mais ça c'est vraiment la définition fondamentale, c'est l'air sous la courbe. Alors vous allez me dire, oui c'est bien, mais les fonctions continue positives, ce n'est pas toutes les fonctions. On va un peu élargir cette définition, vous aurez bien raison de dire ça. On va regarder ce qu'il se passe pour les valeurs négatives. Donc pour les valeurs négatives... Pourquoi ce n'est pas très bien cadré ça ? Je remets ça un petit peu plus droit. Voilà, pour les valeurs négatives, soit f, une fonction continue sur l'intervalle a, b, on appelle intégrale de f sur a, b le nombre écrit de la même manière que tout à l'heure, défini par, si f est positive, i égale l'air de la surface S, et si f est négative, moins r de la surface S. On va mesurer dans ce cas-là, tout rouge, on va mesurer toute cette surface là, on va la calculer, on va compter combien elle vaut, et on va dire que l'intégrale, si ça c'est genre 12 unités d'air, ou 12 cm², mais disons 12 unités d'air, on va dire que l'intégrale c'est moins 12. En fait on va prendre comme norme qu'on a une définition pour les fonctions positives, il n'y a pas de raison de ne pas en avoir pour les fonctions négatives, on va juste calculer la surface et mettre un signe moins. On va considérer que ce sont des surfaces négatives, c'est comme si on pouvait mettre un signe surface, c'est ce qu'on décide de faire pour cette notion d'intégrale. Après il y aura des cas un peu plus mixtes, comme le cas que j'ai mis là-bas, où ce sera quelques bouts qui seront positifs, quelques bouts négatifs. Je peux vous montrer ça d'un peu plus près. Quand on regarde ça un peu plus près, ce qu'on voit, hop j'ai le micro donc chiant, un peu plus près on voit cette fonction, j'ai donc une intégrale positive ici, mais je peux essayer de descendre un petit peu le niveau de cette intégrale, de cette fonction, pour avoir une fonction un peu différente, une cousine à elle si vous voulez, un petit peu décalée vers le bas, qui elle a certaines valeurs de son intégrale, donc de son air sous la courbe, qui vont être considérées comme négatives. Donc si je vais très très bas, on considérerait que cette air là, on va appeler ça une intégrale négative, on va donner la valeur de cette intégrale qui sera moins la valeur de l'air que je peux mesurer, qui elle est toujours positive, donc c'est une air. Et ensuite si on veut le faire un peu pour ce cas là, donc c'est très simple comme on l'a déjà vu, et un mix, on dira juste qu'il y a des parties positives, des parties négatives. Voilà, c'est tout ce que j'ai à dire sur la définition. Je n'ai pas grand chose à ajouter là-dessus, à part sur l'idée que vous avez des graphes en gros qui vont passer au-dessus et en dessous de l'axe OX, il faudra toujours penser que l'intégrale est positive quand on est au-dessus, négative quand on est en dessous, c'est une norme. Voilà, n'hésitez pas à poser des questions dans la FAQ, et je vous retrouve pour la prochaine vidéo.

Définition de l'intégrale

RELATED

Recommended videos

Introduction

Encadrement et intuition graphique