 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie- Physique
- Chimie
- Physique
- Chimie
TerminaleMPSI/PCSI Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie- Physique
- Chimie
- Physique
- Chimie
TerminaleMPSI/PCSI Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Physique-Chimie
Physique
Terminale
Montage afocal
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
Terminale
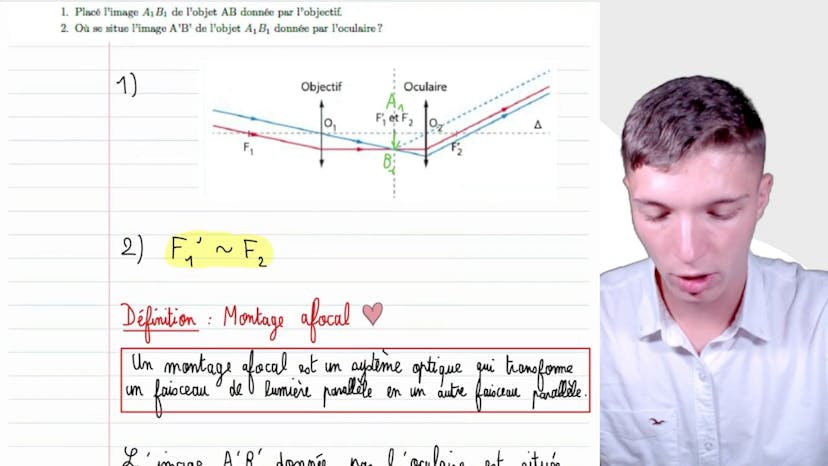
Image intermédiaire
Dans cette vidéo, Mathis explique comment placer une image intermédiaire à l'intérieur d'une lunette astronomique. Il commence par expliquer qu'il a tracé deux rayons issus d'un point B d'un objet AB situé à l'infini. Le point A est situé sur l'axe optique. Ensuite, il faut placer l'image A1, B1 de l'objet AB donné par l'objectif. Pour construire cette image, il faut se placer au niveau du point où les rayons se croisent, c'est-à-dire au niveau du foyer image de l'objectif ou du foyer objet de l'oculaire. A1 et B1 sont donc situés à cet endroit de croisement. L'image intermédiaire est donc bien placée dans la lunette astronomique. Ensuite, la vidéo aborde la question de l'emplacement de l'image A' B' de l'objet A1, B1 donné par l'oculaire. Mathis explique qu'il s'agit d'un montage infocal, ce qui signifie que F1' est confondu avec F2. Cela transforme un faisceau de lumière parallèle en un autre faisceau de lumière parallèle. Par conséquent, l'image A' B' donnée par l'oculaire est située à l'infini. C'est une notion cruciale à comprendre pour la lunette astronomique. À partir de cette image intermédiaire, puisqu'elle est placée au niveau du foyer objet de l'oculaire, elle ressortira à l'infini. En conclusion, Mathis remercie les spectateurs d'avoir suivi la vidéo et leur donne rendez-vous prochainement.
Physique-Chimie
Physique
Terminale
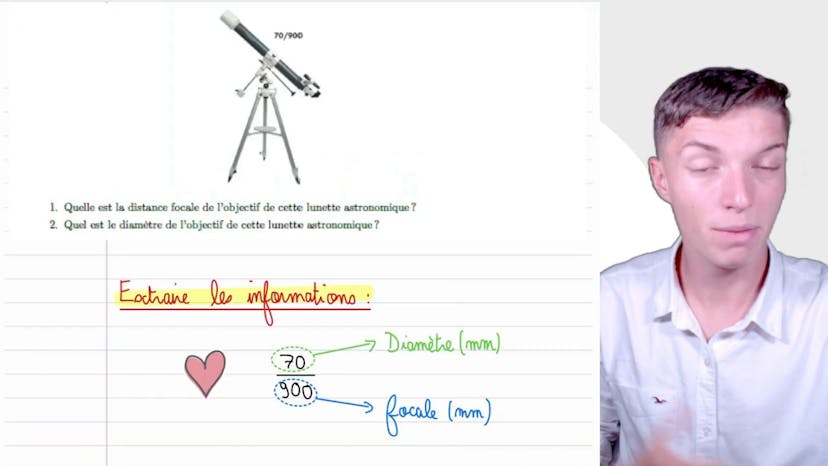
Dimensionnement
Dans cette vidéo, nous apprenons à dimensionner une lunette astronomique à partir de très peu d'informations. Sur la photo du télescope, nous pouvons voir les chiffres "70 sur 900". Pour déterminer la distance focale et le diamètre de l'objectif, nous devons extraire ces informations de ces chiffres. Le numérateur (70) correspond au diamètre de l'objectif, tandis que le dénominateur (900) correspond à la distance focale. Il est important de noter que ces chiffres doivent être adaptés aux unités appropriées, telles que les millimètres. Ainsi, pour cette lunette en particulier, le diamètre de l'objectif serait d'environ 70 millimètres et la distance focale serait d'environ 900 millimètres. Ces dimensions correspondent à celles attendues pour une lunette astronomique de cette taille. N'oubliez pas de retenir cette méthode pour extraire les informations à partir d'une seule grandeur afin de caractériser une lunette astronomique. Merci d'avoir regardé cette vidéo et à bientôt !
Physique-Chimie
Physique
Terminale
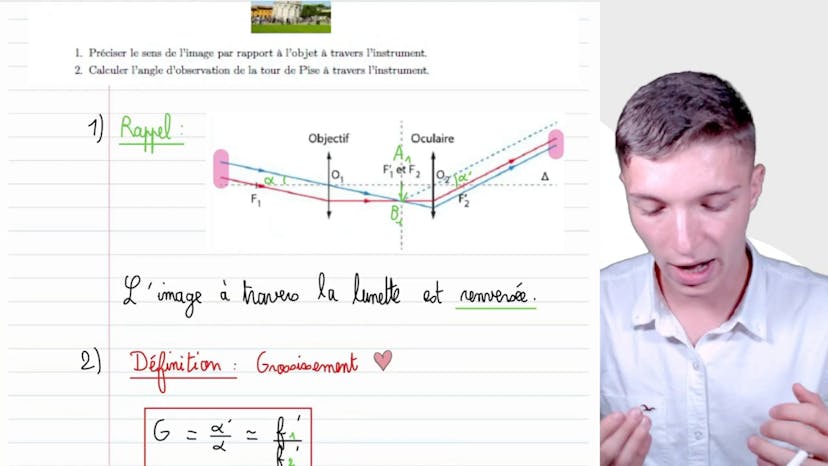
Tour de Pise
Dans cette vidéo, Matisse de Studio nous présente la Tour de Pise observée à travers une lunette astronomique. La distance de l'observation est de 57 mètres et le grossissement de la lunette est de 15. L'image observée à travers la lunette est renversée, ce qui est une caractéristique de ce type d'instrument. Pour calculer l'angle d'observation de la tour à travers la lunette, on utilise la définition du grossissement. Dans cet exemple, la tour a une taille apparente de 3,2 degrés, ce qui donne un angle d'observation de 48 degrés à travers la lunette. Ainsi, on peut observer la tour de Pise de manière beaucoup plus détaillée grâce à cette lunette astronomique. C'est la fin de cet exercice sur les caractéristiques de la lunette astronomique. N'hésitez pas à le revoir et à bientôt !
Physique-Chimie
Physique
Terminale

Anneaux de Saturne
Dans cette vidéo, nous abordons les travaux de Galilée sur les anneaux de Saturne. Le 25 juillet 1610, Galilée observe les anneaux de Saturne avec sa lunette astronomique. Nous cherchons à calculer l'angle d'observation alpha à l'œil nu en utilisant la tangente de cet angle. Nous obtenons un résultat de 7,2 x 10^-4 radian. Nous expliquons ensuite pourquoi les anneaux de Saturne n'ont pas pu être observés avant 1610 en raison de la sensibilité de l'œil humain et de la taille apparente des anneaux. Nous souhaitons ensuite observer l'image à travers la lunette avec un angle alpha prime de 0,10 radian, ce qui nécessite un grossissement de 139. En utilisant la définition du grossissement, nous exprimons le rapport entre les distances focales de l'objectif et de l'oculaire. Sachant que l'oculaire a une focale de 2 cm, nous calculons la distance focale de l'objectif, qui est de 2,78 m. Enfin, en utilisant la formule pour le dimensionnement d'une lunette astronomique, nous déduisons que la lunette doit mesurer au minimum 2,8 m. Voilà comment nous avons résumé ce cours sur les travaux de Galilée sur les anneaux de Saturne en termes SEO-friendly.
Physique-Chimie
Physique
Terminale

Double expression
Dans cette vidéo, Matisse de Studio nous explique le principe du grossissement en optique. Il commence par rappeler que dans une lunette astronomique, il y a un objectif de distance focale f1 prime et un oculaire de distance focale f2 prime. La première étape est de schématiser la situation, en représentant les différents angles du trajet du rayon lumineux.
Ensuite, il montre comment, dans le cadre de petits angles, on peut démontrer que l'angle alpha est égal à a prime, b prime divisé par f1 prime, en utilisant la formule de la tangente. Il explique également que dans l'hypothèse des petits angles, la tangente de l'angle alpha est approximativement égale à l'angle lui-même.
Il montre ensuite comment, dans le même principe, on peut montrer que l'angle alpha prime est égal à a prime, b prime divisé par f2 prime, en utilisant à nouveau la formule de la tangente.
Enfin, il déduit le grossissement g, qui est égal à alpha prime sur alpha, en utilisant les résultats précédents. Il montre que le grossissement est égal à f1 prime divisé par f2 prime.
En résumé, Matisse explique le principe du grossissement en optique, en montrant comment les angles alpha et alpha prime sont liés à la distance focale de l'objectif et de l'oculaire, et comment cela permet de calculer le grossissement.
Physique-Chimie
Physique
Terminale
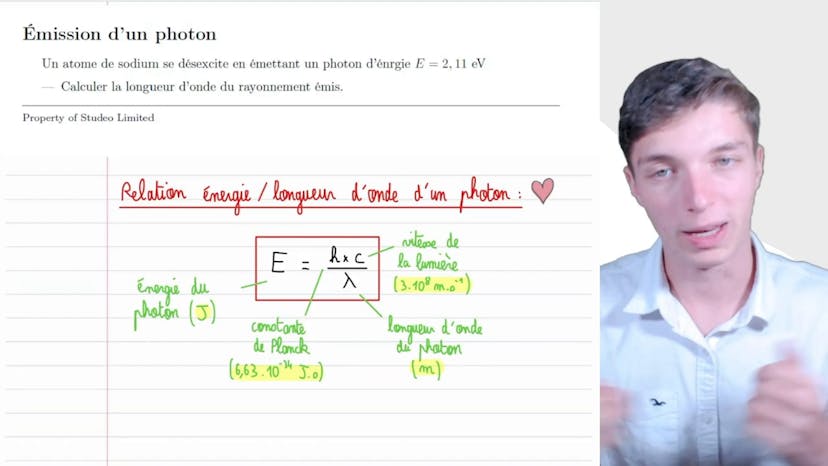
Émission d’un photon
Dans ce cours, Matisse de Studio aborde l'effet photoélectrique et explique l'émission d'un photon. Il explique que tout atome peut émettre un photon, par exemple, un atome de sodium peut émettre un photon d'énergie 2,11 eV. Il explique ensuite comment calculer la longueur d'onde du rayonnement émis en utilisant la relation énergie-longueur d'onde d'un photon, qui est E = h*c/lambda. Il précise que h est la constante de Planck (6,63 * 10^-34 J*s) et c est la vitesse de la lumière (3 * 10^8 m/s). En utilisant cette formule, il calcule que la longueur d'onde est de 589 nanomètres, ce qui correspond à la couleur jaune. Il illustre ce concept d'émission de photons avec un schéma énergétique, montrant comment un atome excité peut se désexciter en émettant un photon avec une certaine énergie et longueur d'onde. Le cours se termine en rappelant l'importance de comprendre la notion de photons et de leur énergie associée dans le contexte des désexcitations d'atomes classiques.
Physique-Chimie
Physique
Terminale

Plaque de sodium
Dans cette vidéo, on aborde l'effet photoélectrique, qui a été découvert par Einstein. On éclaire une plaque de sodium avec un rayonnement de 400 nanomètres. L'effet photoélectrique correspond à l'émission d'électrons par la matière sous l'action de la lumière. Lorsque le photon rencontre l'électron, son énergie est répartie entre le travail d'extraction de l'électron et l'énergie cinétique communiquée. Pour que l'effet photoélectrique soit observable, l'énergie du photon doit être supérieure au travail d'extraction. Dans le cas du sodium, le travail d'extraction est de 3,78 x 10-19 joules. L'énergie du photon est donc de 4,97 x 10-19 joules, ce qui permet l'observation de l'effet photoélectrique. La deuxième question concerne la vitesse d'éjection des électrons. On peut la déterminer en utilisant l'énergie cinétique qui est restante, qui est égale à l'énergie du photon moins le travail d'extraction. En isolant la vitesse d'éjection dans cette équation, on obtient une vitesse de 5,11 x 105 mètres par seconde. Ces exercices permettent de vérifier la compréhension de l'effet photoélectrique.
Physique-Chimie
Physique
Terminale

Plaque de zinc
Dans cette vidéo, nous étudions l'effet photoélectrique appliqué à une plaque de zinc. En 1888, William Ash a observé que lorsqu'une radiation de longueur d'onde de 330 nanomètres charge positivement une plaque de zinc, une radiation de 400 nanomètres ne le permet pas. La première question à expliquer est pourquoi la plaque de zinc se charge positivement. L'effet photoélectrique extrait des électrons de la matière, qui sont chargés négativement. Ainsi, si on extrait des charges négatives de la plaque, elle se charge positivement. Ensuite, nous devons calculer l'énergie des photons associés à chaque radiation en utilisant la relation classique E = H * C / lambda, avec H étant la constante de Planck. Les applications numériques donnent des énergies de 6,03x10^-19 joules et 4,97x10^-19 joules. Nous devons ensuite expliquer pourquoi la radiation de 400 nanomètres ne permet pas à la plaque de zinc de se charger positivement, contrairement à la radiation de 330 nanomètres. Les photons de la radiation de 400 nanomètres ont une énergie plus faible et donc ils n'ont peut-être pas l'énergie suffisante pour extraire les électrons de la plaque de zinc. Il est possible que le travail d'extraction pour le zinc soit supérieur à l'énergie de ces photons mais inférieur à celle de la radiation de 330 nanomètres. C'est la hypothèse à émettre, car l'effet photoélectrique est observable dans un cas mais pas dans l'autre. Merci d'avoir suivi cette vidéo et à bientôt !
Physique-Chimie
Physique
Terminale

Masse de l’électron
Dans cette vidéo, nous utilisons l'effet photoélectrique pour déterminer la masse de l'électron. Nous éclairons une plaque de cuivre en faisant varier la fréquence du rayonnement lumineux incident et mesurons la vitesse des électrons émis pour chaque valeur de fréquence. Nous obtenons un tableau de valeurs avec la fréquence en Hertz et la vitesse en mètre par seconde. L'objectif est de calculer la fréquence seuil du cuivre, qui correspond à l'énergie seuil nécessaire pour que l'effet photoélectrique se manifeste.
En utilisant une relation établie entre la vitesse d'éjection des électrons et la fréquence du rayonnement incident, nous pouvons tracer une courbe de vitesse au carré en fonction de la fréquence. Cette courbe est une droite, ce qui permet de déterminer une relation linéaire entre la vitesse au carré et la fréquence.
En utilisant cette relation linéaire, nous pouvons exprimer la vitesse au carré en fonction de la fréquence dans une expression donnée. Cela nous permet d'identifier deux manières de déterminer la masse de l'électron en utilisant les coefficients de la droite obtenue. En appliquant les calculs, nous obtenons une valeur très proche de la masse de l'électron connue.
En conclusion, cet exercice est très pertinent et intéressant car il nous permet de déterminer la masse de l'électron grâce à l'effet photoélectrique et aux mesures expérimentales.
Physique-Chimie
Physique
Terminale

Calculer des rendements
Dans cette vidéo, nous calculons les rendements de cellules photovoltaïques en fonction de l'éclairement. Le graphique représente la puissance électrique disponible d'un panneau de cellules photovoltaïques de 1,1 m² pour différents éclairements (1000 Wpm², 600 Wpm² ou 200 Wpm²). Lorsque l'éclairement diminue, la puissance électrique disponible diminue également. Le rendement d'une cellule photovoltaïque est défini comme la puissance électrique produite au maximum divisée par la puissance solaire reçue. Nous calculons le rendement maximal pour chaque éclairement et concluons que le rendement d'une cellule est indépendant de l'éclairement reçu. Cette vidéo introduit les notions d'éclairements, de puissance solaire reçue et de puissance électrique convertie. Merci de votre attention et à bientôt !
Physique-Chimie
Physique
Terminale

Photoélectrique/Photovoltaïque
Dans cette vidéo, on aborde le lien entre l'effet photoélectrique et le photovoltaïsme. Le silicium, un semi-conducteur, possède une bande de valence et une bande de conduction qui ne se chevauchent pas. Cependant, leur écart énergétique, appelé gap, est faible, avec une valeur de 1,11 électronvolts.
Le travail d'extraction d'un électron d'un atome de silicium provoquant son ionisation est égal à l'énergie d'ionisation divisée par le nombre d'Avogadro. Cette valeur peut être exprimée en électronvolts et est calculée à 1,31x10^(-18) joules.
La fréquence seuil du silicium, à partir de laquelle l'effet photoélectrique est observable, est calculée en divisant le travail d'extraction par une constante. Sa valeur est de 1,98x10^15 Hertz.
La longueur d'onde maximale de la radiation permettant l'observation de l'effet photoélectrique sur le silicium est calculée en utilisant la relation entre la fréquence seuil et la longueur d'onde. Elle est de 152 nanomètres.
Le diagramme énergétique du silicium représente la bande de valence, la bande de conduction et la bande interdite. Le gap entre la bande de valence et la bande de conduction est représenté par une flèche et est nécessaire pour comprendre le rôle des semi-conducteurs dans le photovoltaïsme.
Lorsqu'un photon d'énergie supérieure ou égale au gap frappe un atome de silicium, il est absorbé, et un courant apparaît dans le cristal, ce qui est l'effet photovoltaïque. La longueur d'onde maximale de la radiation permettant l'observation de cet effet est calculée en utilisant la relation entre l'énergie d'un photon et sa longueur d'onde. Sa valeur est de 1,12 µm.
En résumé, l'effet photoélectrique nécessite une longueur d'onde plus faible que l'effet photovoltaïque. Ces deux phénomènes sont au cœur du chapitre et sont très intéressants à étudier.


