Online Corrigés de BAC Courses by Top Instructors

Un tracteur gravitationnel pour dévier un astéroïde (2)

Dans cette partie du cours, Leïla explique la déviation d'un astéroïde appelé Apophis et son impact sur la Terre. Elle commence par donner l'expression de la norme de la force exercée par l'engin spatial sur Apophis en fonction de gMd. Cette force est de 0,2 N. Ensuite, elle applique la deuxième loi de Newton dans le référentiel héliocentrique pour trouver l'expression de Δt en fonction de Δv, qui est Δt= gm/d^2. Elle explique ensuite que les scientifiques ont estimé qu'il fallait augmenter la norme du vecteur vitesse de 2x10^-6 m/s au niveau de l'aphélie, et demande la durée Δt d'utilisation dans ce cas. En faisant les calculs, elle trouve que Δt est égal à 96 heures ou 4 jours. Leïla indique également que l'utilisation du tracteur gravitationnel augmente le rayon de la trajectoire de l'astéroïde, ce qui affecte la période. Elle établit ensuite la troisième loi de Kepler pour Apophis dans le référentiel héliocentrique, en utilisant le principe fondamental de la dynamique et en raisonnant sur les périodes. Elle obtient l'expression R^3/T^2 = GMs/(4π^2). Ensuite, elle détermine la valeur de la période de révolution T' après l'utilisation du tracteur gravitationnel, en prenant en compte une augmentation de 15 minutes. En utilisant la loi de Kepler, elle calcule le nouveau rayon de la trajectoire, qu'elle trouve être 1,37 x 10^11 mètres. Finalement, elle calcule l'écart de rayon, qui est de 3 x 10^6 mètres, pour montrer le changement de trajectoire de l'astéroïde. Leïla conclut en soulignant l'importance de ces concepts pour comprendre les forces gravitationnelles.

Eclipse solaire du 10 juin 2021 (1)

Dans ce cours, Léa aborde l'exercice sur l'éclipse solaire qui est tombée au Bac l'année dernière en Polynésie. Elle explique que cet exercice fait partie des exercices optionnels du Bac de Physique. Elle souligne également que l'exercice concerne l'optique géométrique et plus particulièrement la lunette astronomique. Léa présente brièvement la lunette astronomique comme un instrument à focale composé de deux lentilles convergentes. Ensuite, Léa passe à la résolution de l'exercice. Elle explique que la première étape consiste à identifier les termes "objectif" et "oculaire" dans la figure de la lunette de Galilée. Elle indique que la lentille L1 est l'objectif car elle est la plus proche de l'objet observé, tandis que la lentille L2 est l'oculaire car elle est proche des yeux. Léa poursuit en demandant aux étudiants de donner le nom scientifique du point P où les rayons se croisent pour la lentille L1. Elle rappelle que les rayons se croisent au foyer principal image de la lentille L1. Ensuite, Léa aborde l'éclipse du 10 juin 2021 et fournit les données techniques de construction de la lunette utilisée. Elle explique qu'il faut positionner le foyer principal objet de la deuxième lentille au même endroit que le foyer principal image de la première lentille pour que la lunette soit afocale. 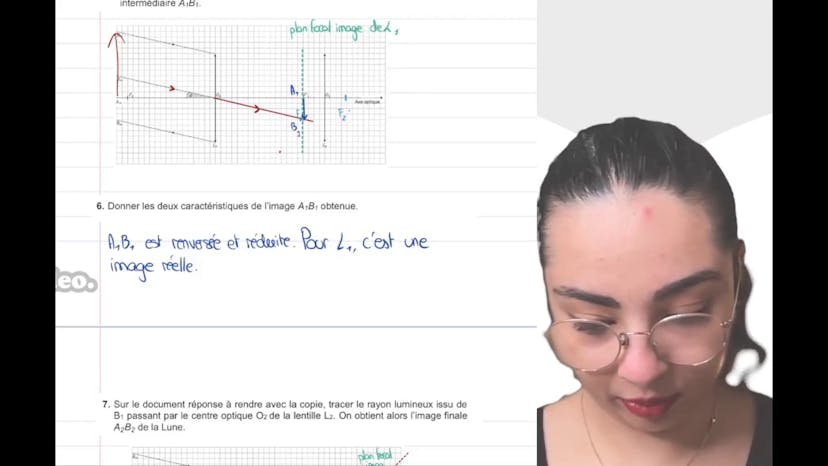Léa répond ensuite à une question sur le passage d'un rayon lumineux issu de B infini à travers le centre optique O1 de la lentille L1. Elle explique qu'un rayon qui traverse le centre optique d'une lentille n'est pas dévié et trace le rayon lumineux correspondant sur un schéma. Léa poursuit en demandant aux étudiants de donner les caractéristiques de l'image obtenue (A1-B1). Elle mentionne que l'image est renversée et réduite, et précise que c'est une image réelle car les rayons se croisent effectivement. Ensuite, Léa demande aux étudiants de tracer le rayon lumineux issu de B1 passant par le centre optique O2 de la lentille L2 pour obtenir l'image finale A2-B2 de la lune. Elle explique que ce rayon-là n'est pas dévié et que son image ressort à l'infini car il se trouve dans le plan focal objet de la lentille L2. Enfin, Léa demande aux étudiants de représenter le faisceau de rayons lumineux issus de B-infini passant par les bords des lentilles L1 et L2. Elle explique que les rayons se croisent tous au point B pour former une image intermédiaire, puis ressortent parallèles car l'objet est à l'infini. Léa conclut en précisant que cet exercice aura été utile et annonce qu'elle continuera la suite dans une prochaine vidéo.

Eclipse solaire du 10 juin 2021 (2)

Dans cette vidéo, Laila termine l'exercice B du sujet Polynésie 2022, jour 1, qui traite de la lunette astronomique. Elle explique qu'il faut positionner l'angle theta prime pour observer l'image finale de la Lune à travers la lunette, et que le grossissement de la lunette est donné par theta prime sur theta. Elle utilise des approximations pour déterminer le grossissement en se basant sur les triangles formés par les lentilles. En utilisant les valeurs des focales de l'objectif et de l'oculaire données dans l'encadré, elle calcule un grossissement de 73, qui est cohérent avec la valeur maximale proposée par le fabricant de la lunette. Ensuite, elle aborde le sujet de l'éclipse et du diamètre de la Lune par rapport au Soleil. Elle utilise des schémas et des calculs trigonométriques pour déterminer le diamètre de la Lune, qui est environ 3,56 fois 10 puissance 3 km. Elle compare cette valeur avec celle donnée dans l'article, qui est d'environ 3,48 fois 10 puissance 3 km, et conclut que l'écart est probablement dû à des approximations dans l'article. Elle termine en encourageant les spectateurs à poser des questions et en annonçant la prochaine vidéo où elle abordera l'exercice C.

Acoustique d’une salle (1)

Le cours aborde la diffraction des ondes lumineuses et sonores dans le contexte de l'acoustique d'une salle. Dans la première partie, on étudie une expérience sur la diffraction des ondes lumineuses, en utilisant un laser et une fente. On détermine que l'angle caractéristique de diffraction est θ = λ/a, où λ est la longueur d'onde et a est la largeur de la fente. On montre ensuite que la largeur de la tâche de diffraction est L = 2λd/a, en utilisant des approximations géométriques. On mesure la largeur L en faisant varier la taille de la fente a, et on obtient une relation linéaire de la forme L = k/a. En utilisant une autre relation donnée dans la question précédente, on exprime k en fonction de λ et D, où D est la distance entre la fente et l'écran. On nous demande ensuite de montrer que λ = 6,5x10^-7 mètres en interprétant un graphique et en calculant le coefficient directeur de la droite correspondante. On détermine également les angles θ1 et θ2 correspondant aux largeurs a1 = 38 micromètres et a2 = 150 micromètres respectivement, en utilisant la formule θ = λ/a. On conclut que la diffraction est plus marquée pour la fente de taille a1, car l'angle de diffraction θ1 est plus grand que θ2. On donne rendez-vous pour la suite du cours dans une prochaine vidéo qui abordera la diffraction sonore.

Acoustique d’une salle (2)

Dans cette vidéo, Layla de Studio aborde la dernière partie de l'exercice C du sujet Polynésie 2022 jour 1, qui traite de la diffraction des ondes sonores. Elle explique que la diffraction des ondes sonores fonctionne de la même manière que celle des ondes lumineuses et cela est étudié à travers l'acoustique d'une salle de concert. Layla commence par expliquer que lors d'un concert, un élève constate qu'il perçoit mieux les sons graves de fréquence f1 (200 hertz) que les sons aigus de fréquence f2 (1 kilohertz). Pour comprendre cela, elle rappelle la formule pour exprimer la longueur d'onde lambda d'une onde sonore en fonction de la vitesse du son V son et de la fréquence f, qui est lambda = V son / f. En utilisant cette formule, Layla montre que les longueurs d'onde lambda 1 (pour f1) et lambda 2 (pour f2) ont des valeurs respectives de 1,70 mètres et 0,340 mètres, en appliquant les valeurs données dans l'énoncé. Ensuite, Layla présente la situation à laquelle l'élève doit réfléchir. Il y a une scène de concert avec un pilier important pour l'étude acoustique. L'élève peut se trouver à trois positions : A, B ou C. Il doit choisir la position qui correspond le mieux à sa perception des sons graves par rapport aux sons aigus. Pour cela, Layla explique que la diffraction joue un rôle crucial. En utilisant le pilier comme obstacle, la diffraction se produit différemment selon les fréquences. Si la largeur du pilier est beaucoup plus petite que la longueur d'onde, la diffraction se produit de manière similaire à celle d'une fente étroite dans une expérience de diffraction de la lumière. Layla explique que les sons graves, avec une longueur d'onde plus élevée (lambda 1 ), seront plus diffractés que les sons aigus, avec une longueur d'onde plus petite (lambda 2). Elle visualise les différentes positions (A, B et C) par rapport au pilier et explique que la position C correspondrait le mieux à la situation décrite par l'élève lors du concert, car les sons graves seront plus diffractés, mais les sons aigus peuvent ne pas être perceptibles. Layla conclut en soulignant que cet exercice nécessite une application des connaissances sur les ondes lumineuses et une analogie avec les ondes sonores. Elle espère que cet exercice a été utile et encourage les personnes à continuer à réviser pour le bac de physique qui approche.

Le colorant E127 (1)

Aujourd'hui, nous allons étudier le colorant E127 à travers un exercice de chimie organique. Ce colorant est utilisé pour teinter certains aliments et est également présent dans les médicaments, notamment dans les révélateurs de plaques dentaires. Dans un premier temps, nous devons déterminer la formule topologique de l'erythrosine (E127) et identifier les familles fonctionnelles associées aux différents groupes caractéristiques présents dans la molécule. Nous trouvons notamment les groupes hydroxyle, carbonyl et carboxyle, correspondants respectivement aux fonctions alcool, cétone et acide carboxylique. Ensuite, nous devons justifier la forme prédominante de l'erythrosine présente dans le révélateur de plaques dentaires. Pour cela, nous devons examiner les pH et les pKa de la molécule. En analysant ces données, nous pouvons établir un diagramme de prédominance et constater que la forme prédominante est H2ERY-. Nous passons ensuite à un dosage spectrophotométrique pour déterminer la concentration en colorant dans le révélateur de plaques dentaires. En utilisant les données expérimentales et la loi de Beer-Lambert, nous pouvons calculer la concentration de la solution S, qui est de 5,5 µmol/L. Cependant, il est essentiel de prendre en compte les étapes précédentes de dilution avant d'obtenir la valeur recherchée, qui est de 2,2 x 10-2 mol/L pour la solution mère. Enfin, nous devons déterminer le titre massique en colorant E127. Pour cela, nous utilisons la formule PM = C0M/Rho, où PM représente le titre massique, C0 la concentration, M la masse molaire et Rho la masse volumique de l'eau. En effectuant les calculs appropriés, nous trouvons que le titre massique est de 1,9%. Il est important de noter que cette valeur est proche de la concentration de 2% mentionnée dans l'énoncé initial, ce qui confirme la justesse de nos calculs. En résumé, cet exercice de chimie organique porte sur la synthèse et l'analyse du colorant E127. Nous avons étudié sa formule topologique, les familles fonctionnelles associées, la forme prédominante dans le révélateur de plaques dentaires, ainsi que sa concentration et son titre massique dans cette solution.

Le colorant E127 (2)

Le cours présente la partie 2 d'une synthèse organique réalisée à partir d'un colorant. Dans cette partie, l'objectif est de synthétiser la molécule recherchée, l'érythrosine, à partir de la fluorescine. Le cours explique les différentes étapes de la synthèse et leur rôle, dont la transformation chimique de synthèse, la filtration et le lavage du solide obtenu, et la mesure de la température de fusion pour identifier le produit de la synthèse. Ensuite, il aborde les facteurs cinétiques pour optimiser la vitesse de formation, notamment le chauffage à reflux. Le réactif limitant de la synthèse de l'érythrosine est déterminé à l'aide d'un tableau d'avancement, en comparant les quantités consommées des réactifs. Le calcul du rendement permet ensuite de déterminer la masse formée expérimentalement. Enfin, le cours conclut en expliquant comment déterminer le nombre de flacons de pH 7 et d'une certaine concentration qui peuvent être fabriqués avec la synthèse réalisée, en convertissant la masse en quantité de matière et en utilisant la concentration et le volume des flacons. Le résumé SEO-friendly de ce cours est le suivant : Le cours présente la deuxième partie d'une synthèse organique de l'érythrosine à partir de la fluorescine. Il explique le rôle des différentes étapes de la synthèse, l'optimisation de la vitesse de formation, la détermination du réactif limitant et la calcul du rendement. Le cours conclut en expliquant comment déterminer le nombre de flacons pouvant être fabriqués avec la synthèse.

Le colorant E127 (3)

Leïla de Studio donne une dernière partie d'un exercice sur le colorant E127, qui concerne la décoloration d'une solution de ce colorant en utilisant de l'eau de Javel. Deux expériences sont réalisées, une avec de l'eau de Javel diluée et l'autre avec de l'eau de Javel pure. La concentration en quantité de matière du colorant est mesurée au cours du temps pour les deux expériences. Dans la première partie de l'exercice, il est demandé de décrire qualitativement l'évolution de la vitesse de disparition du colorant au cours du temps pour l'expérience A. Ensuite, il est demandé de proposer un facteur cinétique expliquant cette évolution. Dans la deuxième partie de l'exercice, il est demandé de déterminer graphiquement le temps de demi-réaction pour l'expérience A et de le commenter. Enfin, il est demandé de proposer une méthode pour optimiser la décoloration du filtre Buchner, en utilisant les informations des expériences A et B. L'utilisation de l'eau de Javel pure est proposée comme méthode pour augmenter la vitesse de réaction.

La physique du jonglage

Aucun résumé n'est disponible pour cette vidéo

Refroidissement d’un fer à cheval

Le cours porte sur le refroidissement d'un fer à cheval en utilisant les principes de la thermodynamique. La première partie du cours traite du chauffage du fer et explique comment calculer la masse et la variation d'énergie interne du fer lorsqu'il est chauffé. On apprend également que lorsque l'énergie interne augmente, cela signifie que l'énergie cinétique microscopique des atomes de fer augmente. La deuxième partie du cours aborde le refroidissement du fer. On examine d'abord le refroidissement à l'air libre en utilisant la loi de Newton pour les transferts thermiques. On applique ensuite le premier principe de la thermodynamique pour trouver l'équation différentielle qui régit l'évolution de la température du fer lorsqu'il perd de la chaleur à l'air. On vérifie ensuite que la fonction proposée dans la solution de l'équation différentielle est bien correcte et on calcule la température du fer après un certain temps. Ensuite, le cours se penche sur le refroidissement du fer dans l'eau. On utilise à nouveau le modèle précédent, mais en prenant en compte le coefficient H de la loi de Newton pour l'eau. On trouve la durée

Défibrilateur cardiaque

Dans ce cours, Leïla présente l'exercice C du bac de l'année précédente qui porte sur un circuit RC modélisant un défibrillateur cardiaque. Le circuit est composé d'un générateur, d'un interrupteur, d'une résistance équivalente à celle du thorax du patient et d'un condensateur. Elle commence par expliquer que pour charger le condensateur, l'interrupteur doit être positionné en position 1, afin de mettre le générateur et le condensateur dans la même boucle. Elle montre ensuite comment obtenir l'équation différentielle en utilisant la loi des mailles et les lois de fonctionnement de chaque composant. L'équation obtenue est : RCDUC/dt + UC = U. Leïla explique ensuite comment vérifier que la solution de l'équation est correcte en utilisant les expressions précédemment obtenues et en les injectant dans l'équation différentielle. Elle montre également comment déterminer le taux de charge (ou taux C) en se basant sur l'argument de l'exponentielle dans la solution. Le taux de charge a la même unité que le temps. 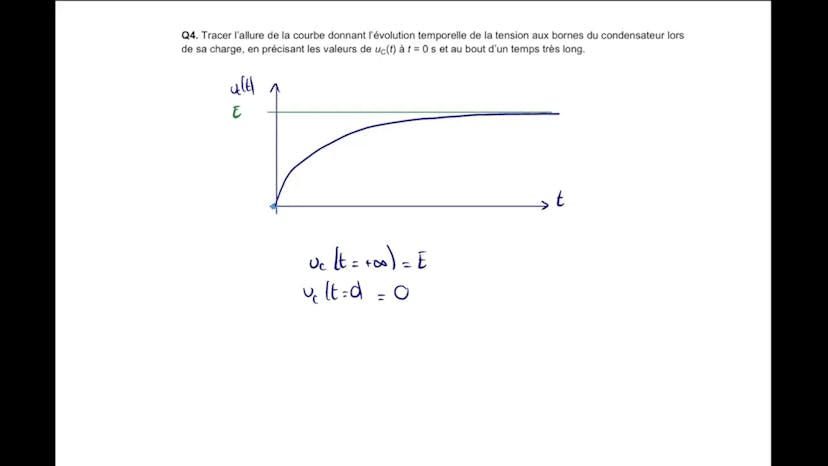Ensuite, Leïla trace la courbe temporelle de l'évolution de la tension du condensateur, montrant qu'elle croît exponentiellement jusqu'à atteindre une valeur finale E. Elle démontre également que le condensateur atteint 99% de sa valeur finale à T1 égale à 5 taux C. Le cours se poursuit avec l'étude de la décharge du condensateur, représentant une défibrillation. Leïla explique comment déterminer graphiquement le moment où l'interrupteur bascule de la position 1 à la position 2, correspondant au début de la décharge. Elle montre également comment obtenir le temps caractéristique de décharge (taux graphe), en traçant la tangente à l'origine et en déterminant son intersection avec l'axe des temps. Enfin, Leïla aborde la durée nécessaire de décharge du condensateur dans des conditions normales d'utilisation. Elle rappelle que la décharge est terminée au bout de 5 taux décharge (5 RC). En utilisant la plage de résistance du corps humain (50 Ohm à 150 Ohm), elle estime que la durée de décharge se situe entre 0,043 secondes et 0,128 secondes, ce qui est bien inférieur aux 4 secondes maximum prévues. Le cours se termine sur l'invitation à regarder les autres vidéos pour les exercices A et B du sujet, puisqu