Indépendance

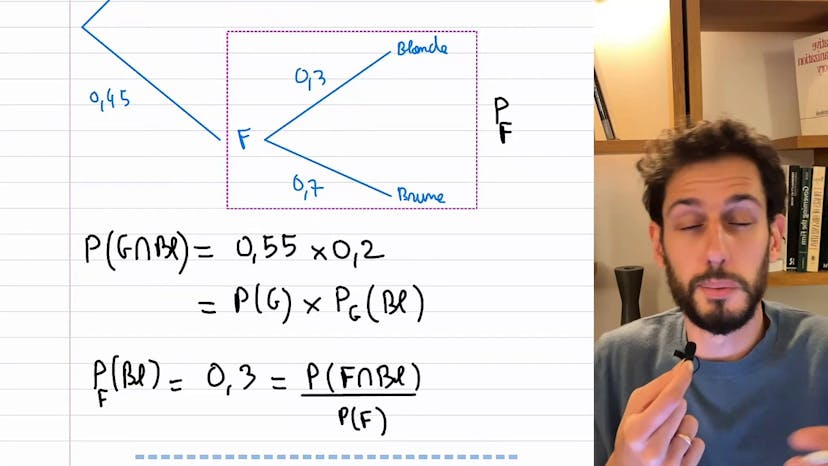
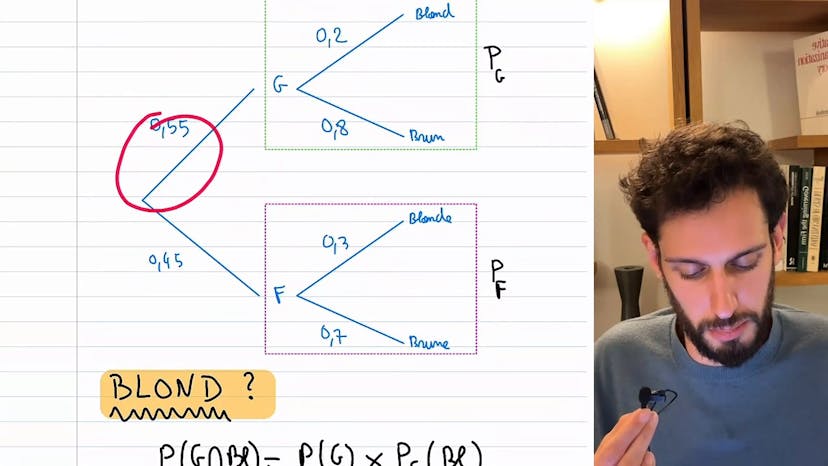
L'indépendance en probabilité est une notion essentielle. Pour comprendre cette notion, il est plus simple de comprendre la dépendance. On peut utiliser deux variables, dans cet exemple, le sexe (garçon ou fille) et la couleur de cheveux (blond ou brun). Pour chaque variable, on peut calculer les probabilités correspondantes. Si on tire un élève au hasard dans un lycée, on peut calculer la probabilité d'être blond en utilisant la formule des probabilités totales. Cependant, cette probabilité dépend du sexe de l'élève. Donc la couleur de cheveux dépend du sexe, ce sont des événements dépendants. Pour illustrer un exemple d'événements indépendants, on peut considérer le fait d'être garçon et blond. Si la proportion de garçons blonds et de filles blondes est la même, peu importe le sexe, cela signifie que la couleur de cheveux est totalement indépendante du sexe. Dans ce cas, les deux événements sont indépendants. La définition formelle des événements indépendants est que la probabilité de l'événement B est la même que la probabilité de B sachant A. Il est également important de comprendre les définitions formelles en mathématiques, même s'il est plus facile de les comprendre à travers des exemples concrets. Une propriété pratique des événements indépendants est que si A et B sont indépendants, alors A barre (le complémentaire de A) B est également indépendant, ainsi que A B barre et A barre B barre. En résumé, l'indépendance des événements en probabilité signifie que la probabilité d'un événement ne dépend pas de la réalisation d'un autre événement.