Application calculatoire

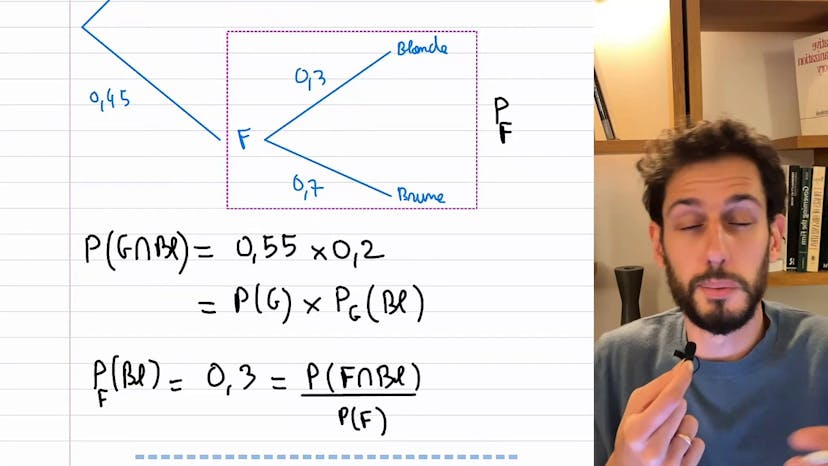
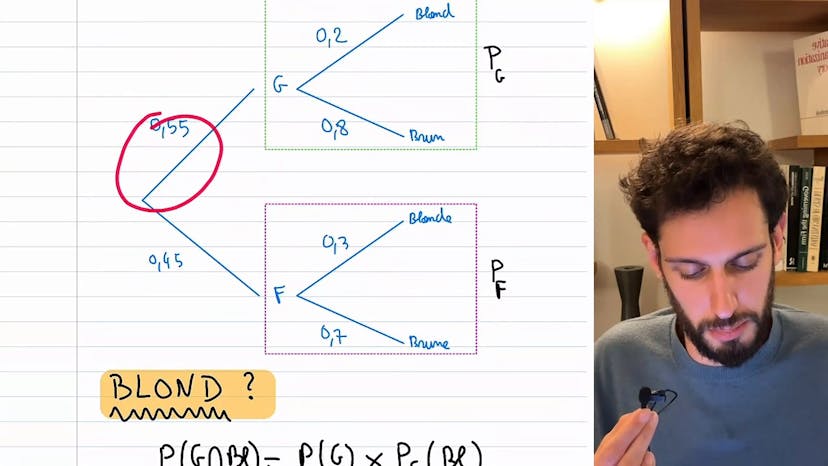
Dans ce cours, nous allons apprendre comment appliquer la formule des probabilités conditionnelles. On nous présente deux événements, A et B, et nous voulons trouver la valeur de P(B|A) en utilisant la formule des probabilités conditionnelles. Cette formule est assez simple : P(B|A) = P(A∩B) / P(A). Dans notre cas, nous avons P(A∩B) égal à 0,3 et P(A) égal à 0,6, donc P(B|A) est égal à 0,3 / 0,6, ce qui donne 1,5. On peut également représenter ces événements sous forme d'arbre avec les branches A, A' (non A), B et B' (non B) pour mieux les visualiser. Cependant, il s'agit ici de l'application la plus basique de la formule. Si vous avez des questions, n'hésitez pas à les poser avant de passer à la prochaine vidéo.