Application avec contexte

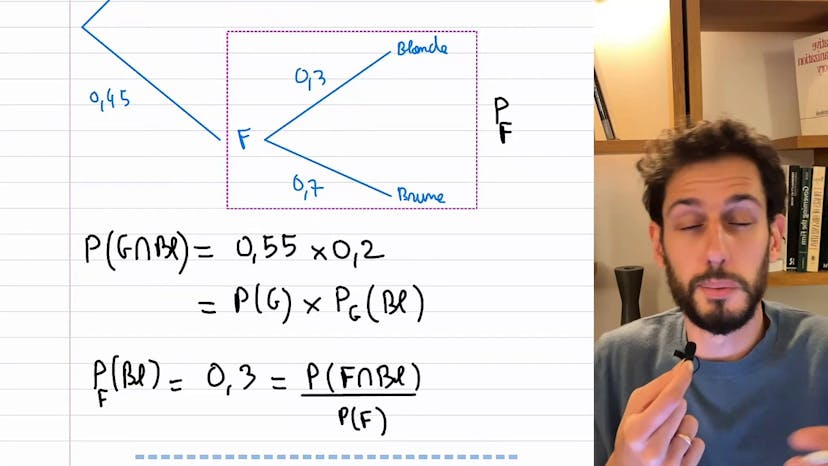
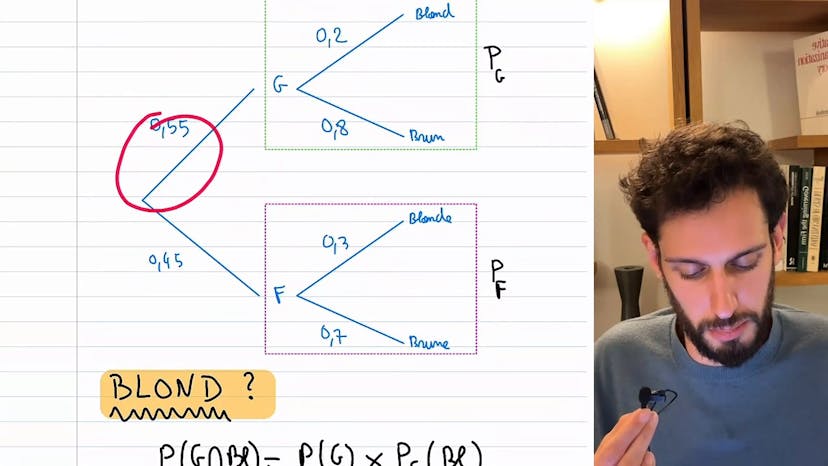
Dans cette transcription vidéo, il est question d'une application utilisant les probabilités conditionnelles. On considère une usine où 60% des voitures fabriquées sont des voitures hybrides, dont 70% sont de marque A. L'objectif est de déterminer la probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de marque A. Le conférencier utilise le concept d'arbre pour représenter les différentes possibilités. Il note que la première partition de l'univers est d'avoir une voiture hybride (60%) ou de ne pas en avoir (40%). Dans le sous-univers des voitures hybrides, il y a celles de marque A ainsi que d'autres marques non spécifiées. En utilisant la formule des probabilités conditionnelles, le conférencier calcule la probabilité recherchée. Il indique que la probabilité d'avoir une voiture hybride de marque A (noté H inter A) peut être calculée en multipliant la probabilité d'avoir une voiture hybride (60%) par la probabilité d'avoir une voiture de marque A sachant qu'elle est hybride (70%, conditionnelle à H). Ainsi, la probabilité recherchée est de 0,6 * 0,7, soit 42%. Le conférencier souligne que ce raisonnement peut sembler intuitif, mais qu'il est important de bien comprendre et appliquer les notions du cours. Il précise qu'il existe d'autres méthodes pour résoudre ce type d'exercice et invite les participants à poser des questions s'ils en ont besoin. Dans l'ensemble, ce cours explique de manière simple et détaillée comment calculer la probabilité qu'une voiture choisie aléatoirement à la sortie d'une usine soit une voiture hybride de marque A, en utilisant les probabilités conditionnelles et en visualisant le problème à l'aide d'un arbre.