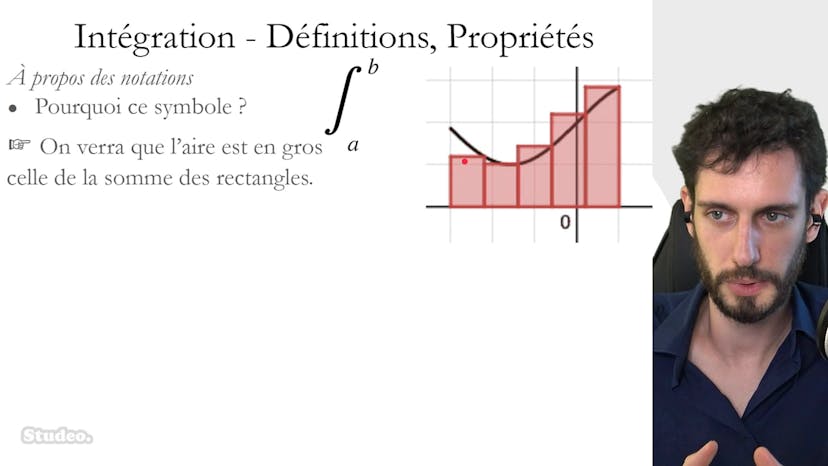
Définition de l'intégrale

L'intégrale d'une fonction continue et positive sur un intervalle a, b correspond à l'aire sous la courbe de cette fonction entre les valeurs a et b, ainsi que l'axe horizontal. On peut également l'appeler le domaine sous la courbe ou l'aire sous la courbe. L'unité utilisée pour mesurer cette aire est l'unité d'air, qui est un petit carré de taille 1 sur 1 dans un repère orthonormé. On note l'intégrale comme une expression mystérieuse "intégrale entre a et b de f de x, dx". Cette définition peut être étendue aux fonctions négatives en calculant la surface correspondante et en lui attribuant un signe négatif. Dans certains cas, il peut y avoir des parties positives et des parties négatives de la fonction. Il est important de se rappeler que l'intégrale est positive lorsque la fonction est au-dessus de l'axe OX et négative lorsqu'elle est en dessous. N'hésitez pas à poser des questions supplémentaires dans la FAQ.