Encadrement et intuition graphique

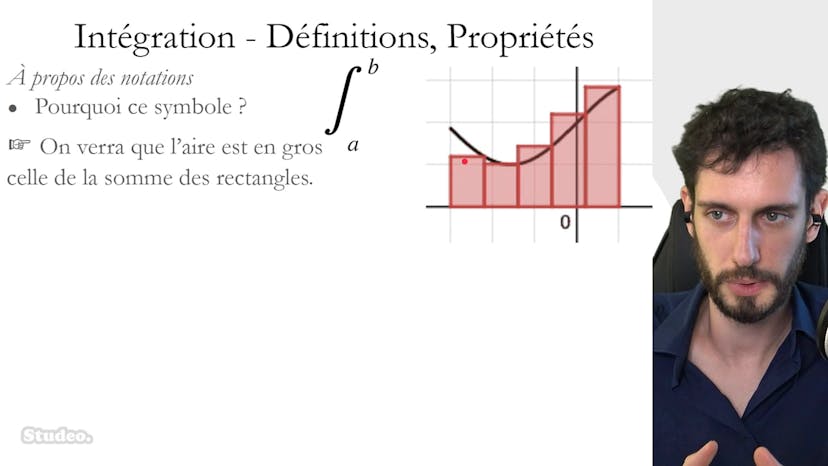
Dans cette vidéo, nous abordons différentes méthodes d'approximation de l'aire sous une courbe. Nous commençons par expliquer que lorsque la courbe est une droite, le calcul de l'aire est assez simple, en utilisant des formes géométriques comme des triangles ou des rectangles. Cependant, lorsque la courbe est incurvée, il devient plus compliqué de calculer l'aire. Nous présentons donc les méthodes d'approximation suivantes : les rectangles supérieurs et inférieurs. Ces méthodes consistent à diviser l'intervalle en plusieurs petits intervalles de même amplitude, et à construire des rectangles inférieurs qui collent la courbe par en dessous, ainsi que des rectangles supérieurs qui collent la courbe par en dessus. Lorsque le nombre de rectangles tend vers l'infini et que leur taille diminue, les rectangles inférieurs et supérieurs convergent vers la vraie valeur de l'aire. En plus de ces méthodes, nous mentionnons brièvement d'autres méthodes qui ne sont pas au programme, mais qui illustrent différentes possibilités : la méthode du point milieu et la méthode des trapèzes. La méthode du point milieu consiste à tracer des rectangles qui sont traversés par la courbe au milieu de leur côté supérieur, offrant ainsi une meilleure précision. La méthode des trapèzes permet quant à elle d'utiliser des quadrilatères non-rectangulaires, offrant ainsi plus de liberté pour se rapprocher de la courbe. En conclusion, cette vidéo explicative présente les différentes méthodes d'approximation de l'aire sous une courbe, en mettant notamment l'accent sur les rectangles supérieurs et inférieurs.