Déterminer le + grand entier

Dans cette vidéo, Corentin aborde un exercice sur les variables aléatoires suivant des lois binomiales. Plus précisément, il cherche à déterminer le plus grand entier cas (k) tel que la probabilité que X soit supérieur ou égal à k est supérieur ou égal à 0,9. Pour résoudre cet exercice, il commence par analyser les phénomènes en jeu. Il remarque que lorsque k augmente, la probabilité que X soit supérieur ou égal à k diminue, car l'ensemble X supérieur ou égal à k devient de plus en plus petit. Ainsi, son objectif est de trouver le cas où la probabilité que X soit supérieur ou égal à k+1 est strictement inférieure à 0,9, tandis que la probabilité que X soit supérieur ou égal à k est supérieur ou égal à 0,9. 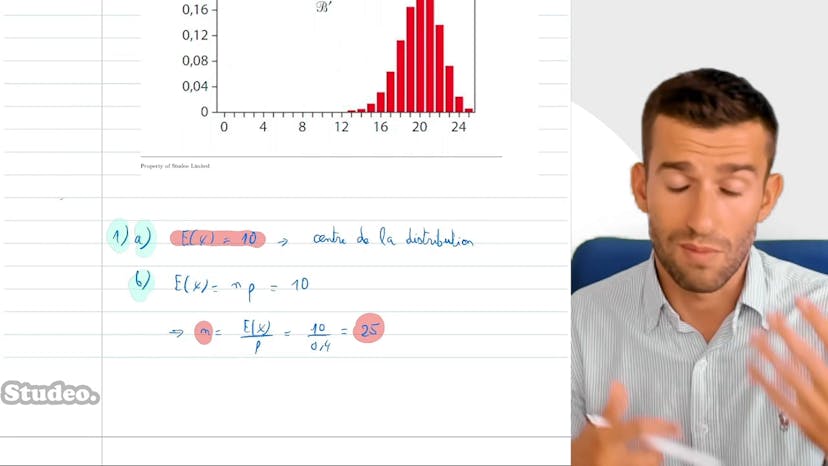En utilisant sa calculatrice, il calcule la probabilité que X soit supérieur ou égal à 22, 21 et 20. Il remarque que la probabilité est égale à 0,80 pour k=22, 0,89 pour k=21 et 0,95 pour k=20. Il constate que pour k=21, la probabilité est strictement inférieure à 0,9, alors que pour k=20, elle est strictement supérieure à 0,9. Il en conclut donc que le plus grand entier k tel que la probabilité que X soit supérieur ou égal à k est supérieur ou égal à 0,9 est 20.