Définition de l'intégrale

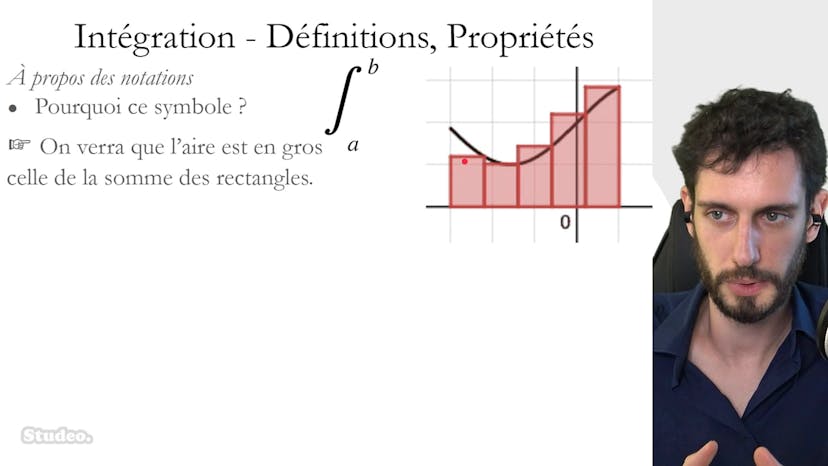
L'intégrale d'une fonction continue et positive sur un intervalle a, b correspond à l'aire sous la courbe de cette fonction entre les axes verticaux x = a, x = b et l'axe horizontal. Elle peut également être appelée "domaine sous la courbe" ou "surface sous la courbe" et est exprimée en unité d'aire. L'unité d'aire est définie comme étant le petit carré de taille 1 entre 0i et 0j dans un repère orthonormé. L'intégrale est notée sous la forme d'un signe mystérieux "∫" suivi de la fonction f(x) et de "dx" pour indiquer la variable d'intégration. Si la fonction f est négative, l'intégrale sera évaluée avec un signe négatif pour représenter une surface négative. Dans certains cas, il peut y avoir des parties positives et négatives, où chaque partie sera évaluée séparément. Il est important de noter que l'intégrale est positive lorsque la fonction est au-dessus de l'axe horizontal et négative lorsqu'elle est en-dessous.