Encadrement et intuition graphique

Dans cette vidéo, nous abordons les différentes méthodes pour approximer l'aire sous une courbe. L'objectif est de mieux comprendre ce qu'est le calcul de l'aire. Nous commençons par expliquer qu'il est facile de calculer l'aire lorsque la courbe est une droite en utilisant des formes géométriques simples telles que des triangles et des rectangles. Cependant, cela devient plus compliqué lorsque la courbe est incurvée. 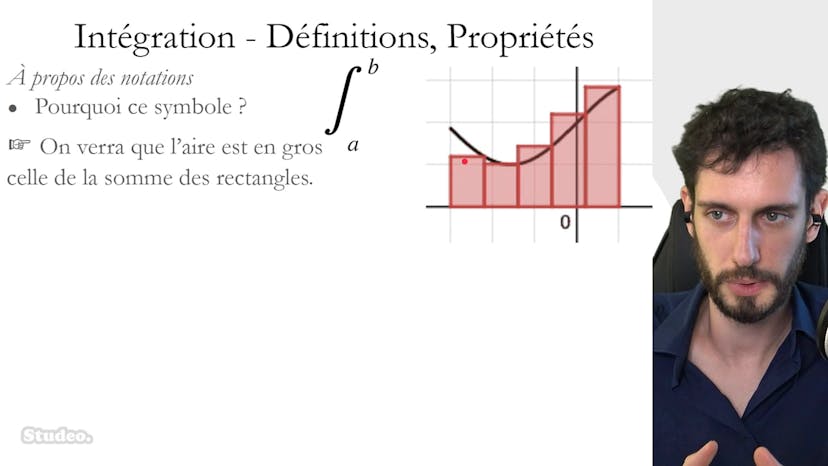Nous présentons ensuite la méthode des rectangles supérieurs et inférieurs, qui est la méthode principale étudiée. Cette méthode consiste à diviser l'intervalle en plusieurs petits intervalles de taille égale et à construire des rectangles inférieurs qui se collent en dessous de la courbe et des rectangles supérieurs qui se collent au-dessus. Lorsque le nombre de rectangles augmente et leur taille diminue, ces rectangles se rapprochent de plus en plus de la courbe, se rapprochant ainsi de la vraie valeur de l'intégrale. Si la fonction est croissante, les aires des rectangles inférieurs et supérieurs sont classées dans un ordre croissant. Nous illustrons ces concepts à l'aide d'un graphique montrant la fonction sinus croissante. Nous utilisons 6 rectangles pour approximer l'aire sous la courbe et montrons comment cette approximation s'améliore en augmentant le nombre de rectangles et en diminuant leur taille. En plus des méthodes au programme, nous mentionnons également la méthode du point milieu et la méthode des trapèzes, qui offrent des approximations plus précises mais ne sont pas étudiées dans ce cours. Nous concluons en résumant que ces méthodes d'approximation permettent de se rapprocher de la vraie valeur de l'intégrale et de mieux comprendre le calcul de l'aire. Si des questions subsistent, nous invitons les spectateurs à les poser dans la FAQ et nous annonçons une prochaine vidéo sur le sujet.