Classique : produit défectueux en usine

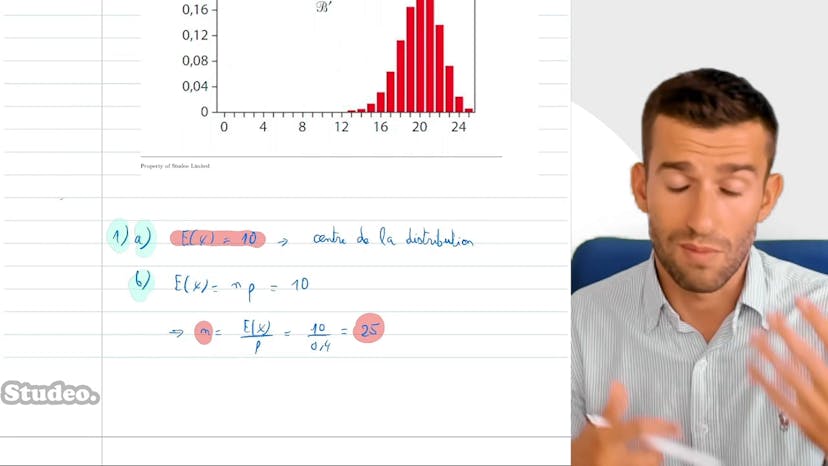
Dans ce cours sur les produits défectueux en usine, nous examinons deux tests indépendants. La probabilité qu'un produit défectueux passe le premier test est de 0,12 et celle pour le deuxième test est de 0,08. Pour qu'un produit soit mis en vente, il doit passer les deux tests, ce qui donne une probabilité de vente de 0,96%. Ensuite, nous nous demandons quelle est la probabilité qu'au moins trois produits défectueux soient mis en vente sur 100 produits indépendants. Nous utilisons la loi binomiale pour modéliser cela, avec une probabilité de réussite de 0,0096. En calculant la probabilité complémentaire, nous trouvons que la probabilité d'avoir au moins trois produits défectueux en vente est de 7%. Ces calculs sont basés sur la formule classique de la loi binomiale, où nous utilisons la combinaison de K parmi N, multipliée par la probabilité de réussite à la puissance K et la probabilité d'échec à la puissance N moins K. J'ai simplifié l'appellation en appelant la réussite la vente, mais cela peut être sujet à débat. Les formules utilisées sont désormais familières et maîtrisées.