Méthode des Rectangles

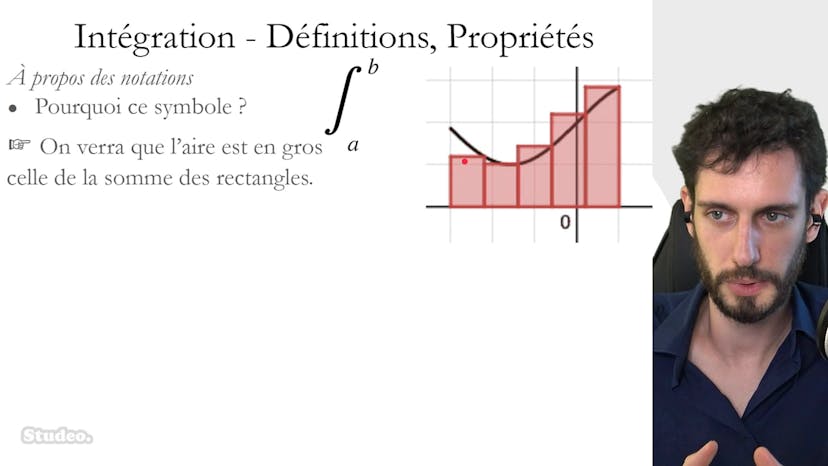
Dans ce cours, nous allons effectuer un calcul d'aire géométrique en utilisant la méthode des rectangles. La courbe intégrée n'a pas une forme géométrique simple, donc nous ne pouvons pas calculer directement l'aire géométriquement. Cependant, nous pouvons l'encadrer en utilisant la méthode des rectangles. La courbe en rouge représente notre courbe et nous voulons trouver l'aire sous cette courbe. Nous pouvons dire que cette aire est plus grande que la somme des aires des petits rectangles situés en dessous de la courbe et plus petite que la somme des aires des grands rectangles situés au-dessus de la courbe. En diminuant la largeur des rectangles, nous affinons notre encadrement et lorsque la largeur tend vers zéro, les deux aires se rapprochent et tendent vers l'aire que nous cherchons, c'est-à-dire l'intégrale. Ce concept est appelé les intégrales de Riemann. Dans cet exemple, nous cherchons à encadrer l'aire sous la courbe de 0 à 4. Comme la fonction f est croissante, nous pouvons l'encadrer en disant que l'aire sous la courbe est plus petite que a'0 + a'1 + a'2 + a'3, qui représente les grands rectangles, et plus grande que les aires a'1, a'2, a'3, qui représentent les petits rectangles. Les aires des rectangles sont faciles à calculer en utilisant la formule largeur fois hauteur. Par exemple, a'1 a une largeur de 1 et une hauteur de f2, qui est la valeur de la fonction f pour x = 1. En utilisant la fonction f qui est la racine de x, nous pouvons calculer que a'1 = 1. Nous continuons de calculer les aires des autres rectangles, et nous trouvons que a'2 = racine de 2 et a'3 = 2. Nous pouvons donc encadrer cette intégrale en disant que l'aire sous la courbe est plus petite que 3 + racine de 2 + racine de 3, et plus grande que 1 + racine de 2 + racine de 3. Cet encadrement n'est pas très précis car nous avons une différence de 2 entre les valeurs maximales et minimales. Cependant, en augmentant la précision en utilisant des rectangles de largeur plus petite, nous pouvons obtenir un encadrement plus fin qui se rapproche davantage de la courbe. En résumé, la méthode d'encadrement des rectangles permet d'approximer l'intégrale d'une fonction lorsque nous ne pouvons pas trouver une primitive de cette fonction. En diminuant la largeur des rectangles, nous affinons notre encadrement et nous approchons de l'aire réelle sous la courbe. Cette méthode est similaire à celle utilisée par les calculatrices pour calculer une aire en approximant par des petits carrés.