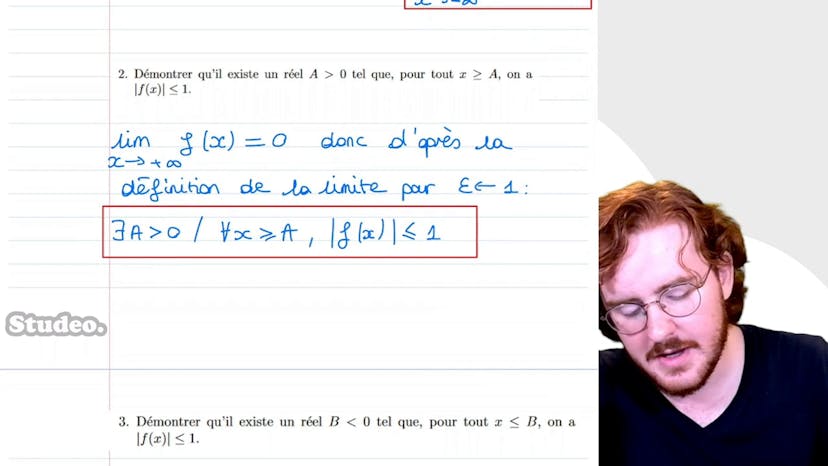
Ensemble image et continuité

Salut, dans ce cours, nous allons montrer que la fonction f est continue sur le segment AB. Pour cela, nous allons supposer par l'absurde qu'il existe un point x0 dans A et B où f n'est pas continue. Comme f est croissante et bornée sur A et B, les limites L- et L+ existent et sont finies. Si f était continue en x0, alors L- serait égal à L+. Cependant, puisque f n'est pas continue en x0, L- est différent de L+. En utilisant la croissance de f, nous pouvons montrer que pour tout x dans A et x0, f(x) est inférieur ou égal à L-. De même, pour tout x dans x0 et B, f(x) est supérieur ou égal à L+. Comme L- et L+ sont différents, il existe un alpha compris entre L- et L+ qui n'appartient pas à l'image de f sur AB. Cependant, alpha appartient à AB, ce qui crée une contradiction. Par conséquent, f est continue sur le segment AB. C'est la fin du cours, à bientôt !