Inégalité fondamentale

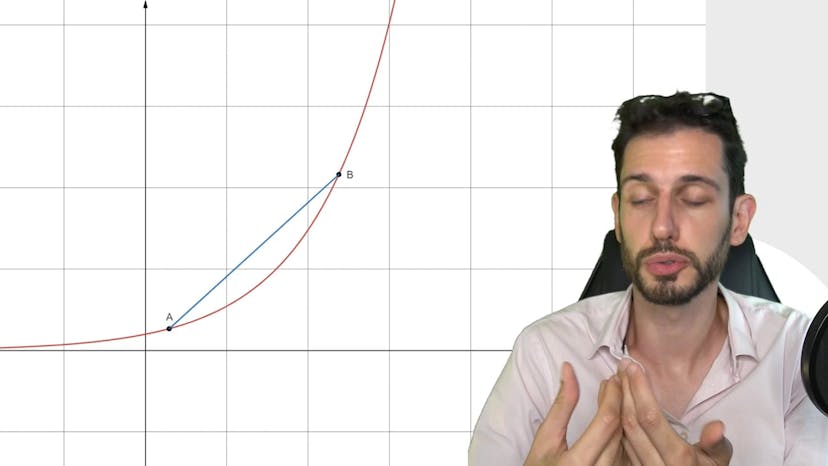
Dans cette vidéo, nous allons étudier la relation entre une courbe et ses sécantes pour traduire la convexité d'une fonction. Une fonction convexe est située en dessous de ses sécantes. Pour illustrer cela, nous avons un graphique avec une courbe rouge située sous les sécantes bleues. L'objectif est de comparer la différence d'ordonnée entre un point sur la sécante bleue et un point sur la courbe rouge pour une même abscisse entre les points A et B. En prenant une abscisse intermédiaire, représentée par le point T, nous pouvons démontrer que le point sur le segment est plus haut que le point sur la courbe rouge. Ainsi, nous concluons qu'il y a une inégalité entre ces deux points. En utilisant cette notion, nous pouvons considérer un point d'abscisse intermédiaire entre A et B, que nous appelons T, en pondérant les abscisses de A et B. En observant l'image de ce point T par la fonction courbe, notée F, nous constatons qu'elle est inférieure à l'image de cette abscisse par l'équation de la sécante. Il peut être difficile de comprendre cette équation rapidement, mais nous pouvons fournir une démonstration complète pour ceux qui sont intéressés. En résumé, cette vidéo explique comment traduire la relation entre une courbe et ses sécantes dans le contexte de la convexité d'une fonction. De plus, il est important de noter le lien logique entre la convexité et la concavité : si F est convexe, alors moins F est concave, et vice versa. Une démonstration complète est disponible dans une autre vidéo. Si vous avez des questions, n'hésitez pas à les poser sur le forum. Merci de votre attention et rendez-vous dans la prochaine vidéo.