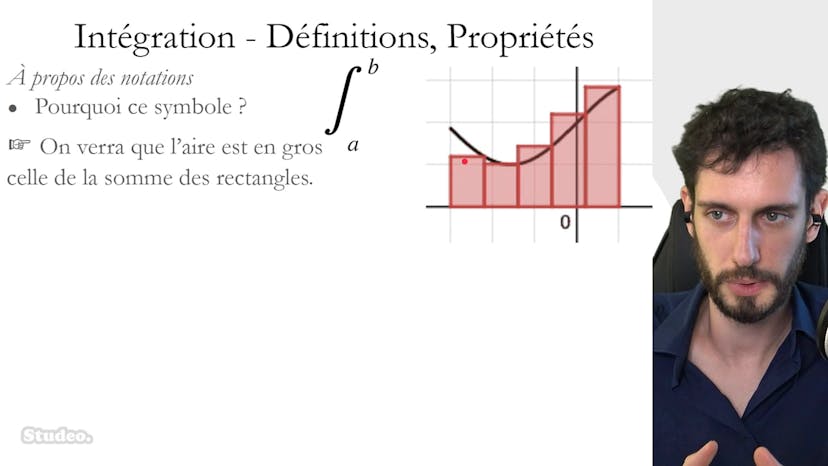
Définition de l'intégrale

L'intégrale d'une fonction continue et positive sur un intervalle [a, b] représente l'aire sous la courbe de cette fonction entre les valeurs x = a et x = b, ainsi que l'axe horizontal. On exprime cette aire en unités d'aire, qui sont des carrés de taille 1 sur 1 dans un repère orthonormé. L'intégrale est notée par le symbole mystérieux entre a et b de f(x) dx. Si la fonction est négative, on considère l'aire comme négative et on met un signe moins devant la valeur de l'aire calculée. Si la fonction présente des parties positives et des parties négatives, on comptabilise les aires séparément. Il est important de noter que l'intégrale est positive lorsque la fonction est au-dessus de l'axe horizontal et négative lorsqu'elle est en dessous.