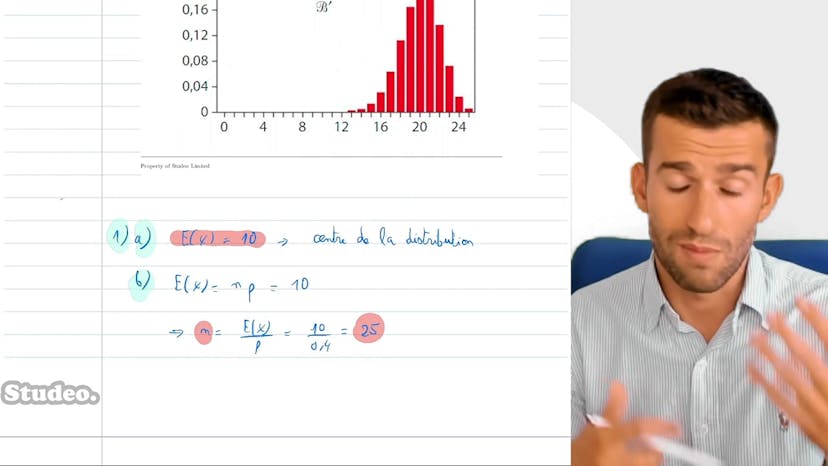
Schéma de Bernoulli

La loi binomiale permet de calculer les probabilités dans des situations où il y a répétition indépendante d'une expérience avec deux résultats possibles : succès ou échec. Pour utiliser cette loi, il faut suivre quelques étapes. Tout d'abord, repérer un chemin de Bernoulli, c'est-à-dire une expérience répétée plusieurs fois indépendamment. Ensuite, attribuer une variable aléatoire x qui représente le nombre de succès. Cette variable suit une loi binomiale de paramètres n et p, où n est le nombre de répétitions et p est la probabilité de succès. Pour calculer la probabilité que x soit égal à k, on utilise la formule suivante : k parmi n fois p à la puissance k, multiplié par 1 moins p à la puissance n moins k. Appliquons ces étapes à un exemple concret. Supposons que nous effectuons des tirages successifs et indépendants de boules, et que notre succès est de tirer une boule noire. Le paramètre de la loi binomiale est alors de 3 boules noires sur 8 boules, ce qui équivaut à une probabilité de réussite de 3/8. En appelant x le nombre de boules noires obtenues, x suit une loi binomiale de paramètres n égal à 5 (car nous faisons 5 tirages) et p égal à 3/8. En utilisant la formule, nous pouvons calculer la probabilité que x soit égal à 3 : 3 parmi 5 fois (3/8) à la puissance 3, multiplié par 1 moins (3/8) à la puissance 5 moins 3. Les calculs nous donnent une probabilité de 20%. C'est ainsi que l'on reconnaît et utilise la loi binomiale pour effectuer des calculs de probabilité. Si vous avez des questions supplémentaires, consultez la FAQ.