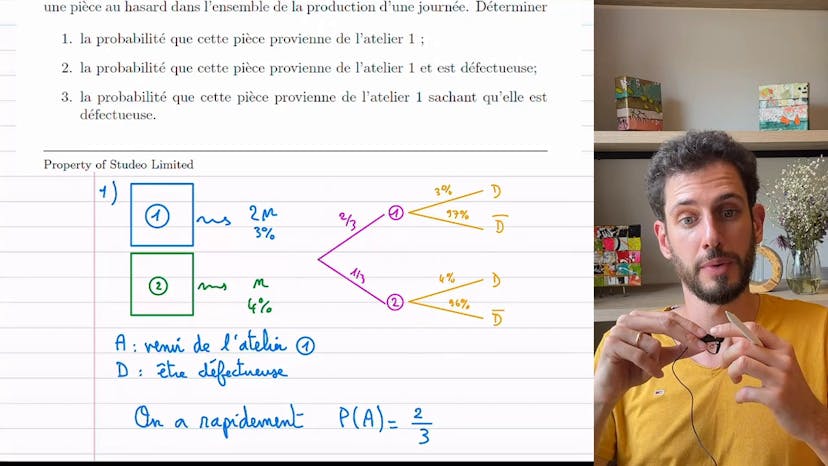
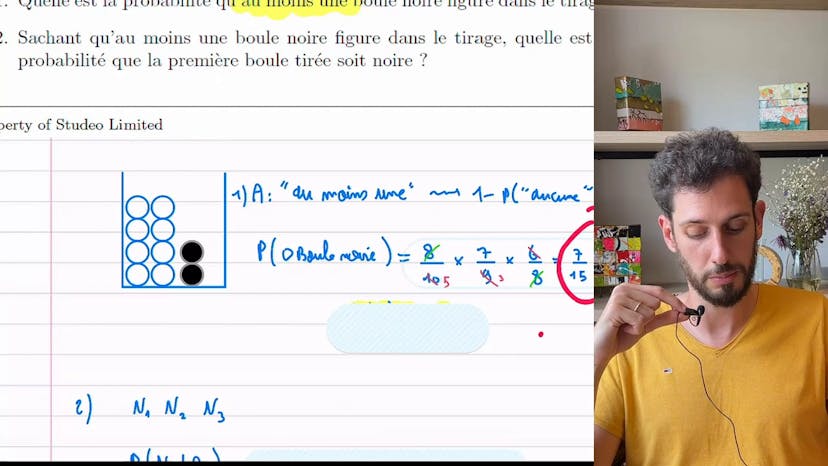
Dés pipés

Dans cet exercice de probabilités intéressant, nous avons 100 dés, parmi lesquels 25 sont pipés et permettent de gagner plus facilement. Chaque dé pipé a une probabilité de 1,5 d'obtenir un 6, tandis que les autres dés ont une probabilité de 1/6. Lorsque nous tirons un dé au hasard et obtenons un 6, nous voulons savoir quelle est la probabilité que le dé soit pipé. Pour cela, nous utilisons l'arbre des probabilités et utilisons les notations suivantes : P pour le dé pipé, et 6 pour obtenir un 6. Nous avons 1 chance sur 4 (25 sur 100) d'obtenir un dé pipé, et donc 3 chances sur 4 d'obtenir un dé non pipé. En ce qui concerne les probabilités d'obtenir un 6, pour les dés pipés, c'est 1,5, et pour les dés non pipés, c'est 1/6. Maintenant, nous voulons calculer la probabilité d'avoir un dé pipé sachant que nous avons obtenu un 6. Pour cela, nous utilisons la formule de la probabilité conditionnelle en utilisant les probabilités intermédiaires : P(inter 6) = 1,25 x 1,5, et P(6) = P(inter 6) + P(inter 6 complémentaire) = 1,25 + 3,25 x 1,5. En simplifiant, nous obtenons une probabilité finale de 1,25. Ainsi, lorsque nous obtenons un 6, la probabilité que le dé soit pipé est de 1,25, soit 1 chance sur 2. Maintenant, nous passons à un scénario plus complexe. Supposons que nous tirions un dé au hasard parmi les 100 dés et que nous le lancions n fois, obtenant chaque fois un 6. Nous voulons maintenant calculer la probabilité que le dé soit pipé. Dans ce cas, nous avons toujours 1/4 de chance d'obtenir un dé pipé et 3/4 de chance d'obtenir un dé non pipé. Pour les dés pipés, la probabilité d'obtenir un 6 n fois est de 1,5^n, tandis que pour les dés non pipés, elle est de (1/6)^n. Pour calculer la probabilité que le dé soit pipé sachant que nous avons obtenu un 6 n fois, nous utilisons la formule de Bayes. Nous obtenons P(n) = (1/2)^n / [(1/4)(1/2)^n + (3/4)(1/6)^n]. En simplifiant cette expression, nous arrivons à P(n) = 1 / (1 + (3/2)^n). Il est important de noter que cette probabilité diminue à mesure que le nombre de fois où nous obtenons un 6 augmente. En fin de compte, si nous avons obtenu un 6 n fois, la probabilité que le dé soit pipé tend vers 0, ce qui signifie qu'il est très peu probable que le dé soit pipé dans ce scénario.