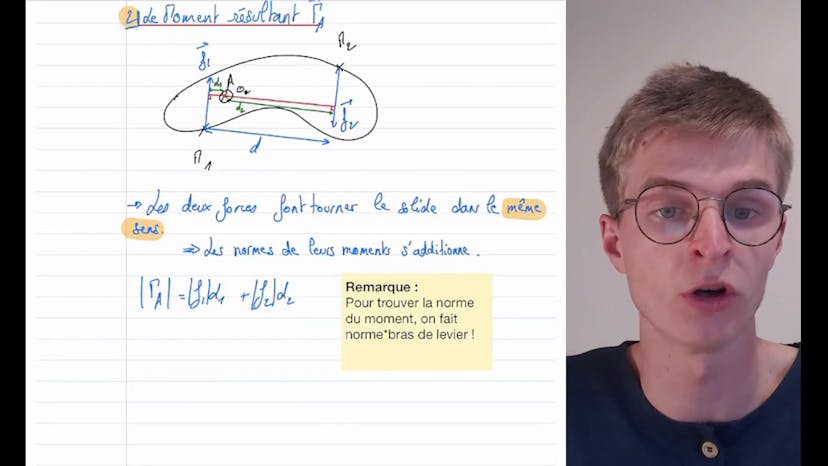
Energie mécanique du pendule pesant

Dans cette vidéo, Théobald de Studio nous parle du pendule pesant et de son énergie mécanique. Il commence par décrire les différentes caractéristiques du pendule, telles que le moment d'inertie (J), le centre de gravité (G) et la distance entre G et l'axe des zéros (D). Il énonce ensuite les questions qui seront traitées dans l'exercice. La première question concerne l'énergie cinétique du pendule. Théobald explique que l'énergie cinétique d'un solide en rotation autour d'un axe fixe est égale à 1,5 de Jθ², où θ est l'angle de rotation du pendule. Ensuite, il aborde l'énergie potentielle du pendule. Il explique que cette énergie est égale à mgd(1-cosθ), où m est la masse du pendule, g est l'accélération due à la gravité, d est la distance entre G et l'axe des x, et θ est l'angle de rotation. Théobald explique alors pourquoi l'énergie mécanique du pendule est constante au cours du mouvement. Il explique que cela est dû au fait que les seules forces agissant sur le pendule sont le poids (une force conservative) et l'action de la liaison pivot (qui ne travaille pas). Par conséquent, l'énergie mécanique est une intégrale première du mouvement. La troisième question porte sur l'équation différentielle du mouvement du pendule. Théobald montre comment dériver l'expression de l'énergie mécanique par rapport à θ pour obtenir cette équation du mouvement. Ensuite, il explique comment tracer le profil d'énergie potentielle du pendule et comment trouver les positions d'équilibre. Il montre que ces positions d'équilibre sont stables lorsque la dérivée de l'énergie potentielle par rapport à θ est positive, et instables lorsque cette dérivée est négative. Il discute ensuite des deux comportements possibles du pendule. Si l'énergie mécanique est inférieure à 2mgd, le pendule oscille entre deux positions extrêmes et a un comportement pendulaire. Si l'énergie mécanique est supérieure à 2mgd, le pendule peut prendre toutes les valeurs d'énergie potentielle et effectuer des tours complets, ce qui correspond à un comportement révolutif. En conclusion, Théobald souligne l'importance de bien comprendre tous les concepts abordés dans cet exercice, car ils sont récurrents et utiles dans le domaine du pendule pesant. Il encourage les spectateurs à poser des questions et annonce une prochaine vidéo à venir.