Pot de confiture

Dans cette vidéo, Matisse de Studio parle de l'utilisation d'un pot de confiture. Il explique que pour remplir le pot, on verse de la confiture à une température de 105°C et à une pression atmosphérique de 1 bar. Le pot a un diamètre de 82 mm et on laisse un espace entre la confiture et le bord du pot. L'air emprisonné entre le couvercle et la confiture est considéré comme un gaz parfait à une température T1. 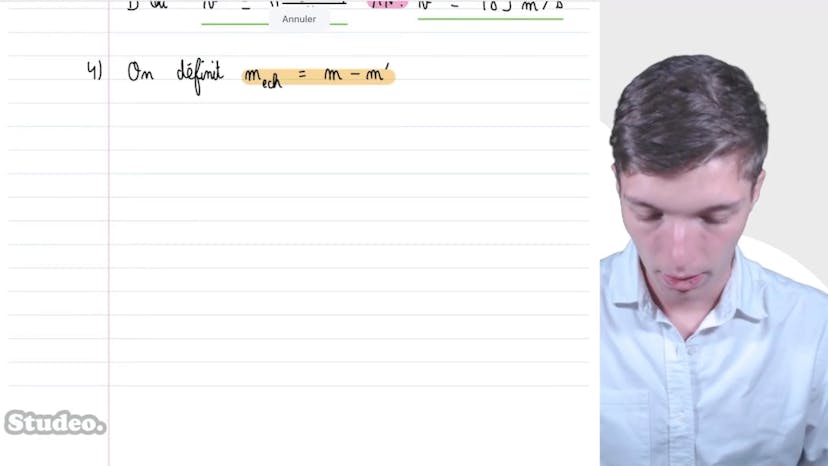Le pot de confiture refroidit lentement jusqu'à atteindre une température de 20°C, et on souhaite déterminer la pression P2 à l'intérieur du pot à ce moment-là. Pour résoudre ce problème, Matisse applique la méthode classique de résolution thermodynamique. Il considère l'air à l'intérieur du pot comme le système et utilise l'équation d'état d'un gaz parfait (P1V = NAR T1) pour établir une relation entre la pression initiale (P1) et la température initiale (T1), et la pression finale (P2) et la température finale (T2). Il trouve finalement que la pression P2 est égale à 0,78 bar. Ensuite, Matisse aborde la seconde question qui consiste à déterminer la résultante des forces de pression sur le couvercle du pot une fois qu'il est refroidi. Il explique que pour relier la pression aux forces de pression, il faut connaître la définition de la force de pression. La force de pression sur une surface est donnée par P fois la surface fois la normale sortante de la surface. En prenant en compte la pression intérieure et la pression extérieure, Matisse trouve que la force sur le couvercle est égale à la valeur absolue de la différence entre la pression intérieure et la pression extérieure, multipliée par la surface du couvercle. En effectuant les calculs numériques, il obtient une force de 1,2 10-3 N due à cette différence de pression. Matisse explique que cela rendra plus difficile l'ouverture du pot, car la pression intérieure est inférieure à la pression extérieure. Il souligne que cela est dû aux forces de pression et à la sous-pression à l'intérieur du pot. Ces forces peuvent rendre encore plus difficile l'ouverture si le pot est sous vide. Il conclut en encourageant les spectateurs à comprendre pourquoi il est plus difficile d'ouvrir un pot en se basant sur la formule PxS (force de pression = pression fois surface) et en faisant des schémas pour mieux visualiser les concepts. En résumé, cette vidéo explique comment remplir un pot de confiture, comment calculer la pression à l'intérieur du pot une fois qu'il est refroidi, et comment les forces de pression affectent l'ouverture du couvercle du pot.